题目内容
3．
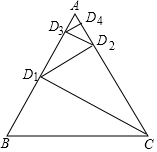某同学用一等边三角形木板制作一些相似的直角三角形．如图，其方法是：过C点作CD1⊥AB于D1，再过D1作D1D2⊥CA于D2，再过D2作D2D3⊥AB于D3…，若△ABC的边长为a，则CD1=$\frac{\sqrt{3}}{2}$a，D1D2=$\frac{\sqrt{3}}{4}$a，D2D3=$\frac{\sqrt{3}}{8}$a，依此规律，则D5D6的长为$\frac{\sqrt{3}}{64}$a．
分析 把CD1、D1D2、D2D3的分母写成2n的形式，从中找出规律，根据规律解答．
解答 解：CD1=$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{{2}^{1}}$a，
D1D2=$\frac{\sqrt{3}}{4}$a=$\frac{\sqrt{3}}{{2}^{2}}$a，
D2D3=$\frac{\sqrt{3}}{8}$a=$\frac{\sqrt{3}}{{2}^{3}}$a，
则D5D6的长为：$\frac{\sqrt{3}}{{2}^{6}}$a=$\frac{\sqrt{3}}{64}$a，
故答案为：$\frac{\sqrt{3}}{64}$a．
点评 本题考查的是相似三角形的性质、等边三角形的性质，掌握相似三角形的对应边成比例是解题的关键．
练习册系列答案
相关题目
9．
如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（ ）
如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（ ）| A． | 7.2 cm | B． | 5.4 cm | C． | 3.6 cm | D． | 0.6 cm |
18．
有这样一个问题：探究函数y=x-$\frac{2}{x}$的图象和性质．
小石根据学习函数的经验，对此函数的图象和性质进行了探究．
下面是小石的探究过程，请补充完整：
（1）函数的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
求m的值；
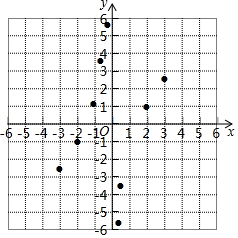
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出此函数的图象；
（4）进一步探究，结合函数的图象，写出此函数的性质（一条即可）：当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而增大．
有这样一个问题：探究函数y=x-$\frac{2}{x}$的图象和性质．小石根据学习函数的经验，对此函数的图象和性质进行了探究．
下面是小石的探究过程，请补充完整：
（1）函数的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{7}{3}$ | -1 | 1 | $\frac{7}{2}$ | $\frac{17}{3}$ | -$\frac{17}{3}$ | -$\frac{7}{2}$ | m | 1 | $\frac{7}{3}$ | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出此函数的图象；
（4）进一步探究，结合函数的图象，写出此函数的性质（一条即可）：当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而增大．
已知函数y1=x2-2x-3．