题目内容
5.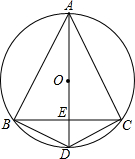 如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.
如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.(1)证明△ABE∽△CDE;
(2)若DE=3,BC=8,求sin∠BAD的值.
分析 (1)利用同弧所对的圆周角相等得到一对角相等,再由对顶角相等,利用两对角相等的三角形相似即可得证;
(2)由三线合一性质得到AD垂直于BC,且BE=CE,求出CE的长,在直角三角形EDC中,利用勾股定理求出CD的长,利用锐角三角函数定义求出sin∠BCD的值,即为sin∠BAD的值.
解答 (1)证明:∵∠BAD与∠BCD都对$\widehat{BD}$,
∴∠BAD=∠BCD,
∵∠AEB=∠CED,
∴△ABE∽△CDE;
(2)解:∵△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,
∴AD⊥BC,BE=CE=$\frac{1}{2}$BC=4,
在Rt△EDC中,DE=3,CE=4,
根据勾股定理得:CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴sin∠BCD=$\frac{DE}{CD}$=$\frac{3}{5}$,
∵∠BAD=∠BCD,
∴sin∠BAD=sin∠BCD=$\frac{3}{5}$.
点评 此题考查了相似三角形的判定与性质,等腰三角形的性质,以及圆周角定理,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.设x是实数,y=|x-1|+|x+1|,下列结论正确的是( )
| A. | y没有最小值 | |
| B. | 只有一个x使y取到最小值 | |
| C. | 有有限多个x(不止一个)使y取到最小值 | |
| D. | 有无穷多个x使y取到最小值 |
15.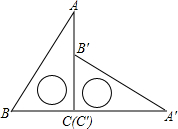 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )| A. | 6cm | B. | (6-2$\sqrt{3}$)cm | C. | 3cm | D. | (4$\sqrt{3}$-6)cm |
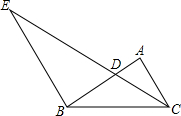 如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为2$\sqrt{10}$.
如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为2$\sqrt{10}$. 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息回答下列问题:
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息回答下列问题: 如图△ABC的周长是30cm,把△ABC的边AC对折,使点C和点A重合,折痕是DE交BC和AC于D点和E点,连接AD,若EC=4cm,△ABD的周长是22cm.
如图△ABC的周长是30cm,把△ABC的边AC对折,使点C和点A重合,折痕是DE交BC和AC于D点和E点,连接AD,若EC=4cm,△ABD的周长是22cm. 如图,画出四边形ABCD关于点O的对称图形.
如图,画出四边形ABCD关于点O的对称图形.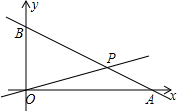 在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标.
在如图所示的直角坐标系中,O为原点,直线y=-$\frac{1}{2}$x+8与x轴、y轴分别交于A、B两点,设直线OP与线段AB相交于P点,且$\frac{{S}_{△AOP}}{{S}_{△BOP}}$=$\frac{1}{3}$,试求点P的坐标.