��Ŀ����
6����ͼ����֪��ABC�У���B=90�㣬AB=8cm��BC=6cm����1����P��Q�ǡ�ABC���ϵ��������㣬���е�P��A��A��B�����˶����ٶ�Ϊÿ��1cm����Q��B��B��C�����˶����ٶ�Ϊÿ��2cm������ͬʱ�����������ʱ��Ϊt�룮
�ٵ�t=1��ʱ����PQ�ij���
�ڴӳ��������Ӻ�PQB�ǵ��������Σ�
��2����M�ڡ�ABC������B��A��C������ÿ��3cm���ٶ��˶�����M�ڱ�CA���˶�ʱ�����BCM��Ϊ����������ʱM�˶���ʱ�䣮
���� ��1�����ݹ��ɶ�����ɣ�
��2����PQB�ǵ��������Σ���B=90�㣬��֪BP=BQ����t��ʾ��BP��BQ�ij����г���ʽ���ɽ��
��3��������������ۣ���BC=BMʱ����MC=MBʱ����CB=CMʱ���г����̽�ɣ�
���  �⣺��1����ͼ1��
�⣺��1����ͼ1��
�ߵ�t=1ʱ��AP=1��BP=7��BQ=2
��PQ=$\sqrt{{PB}^{2}+{QB}^{2}}$=$\sqrt{53}$��
��2���ߡ�PQB�ǵ��������Σ���B=90�㣬
��BP=BQ��
BP=8-t��BQ=2t��
��8-t=2t��
���t=$\frac{8}{3}$��
��3����BC=BMʱ��t=2
��MC=MBʱ��t=$\frac{13}{3}$��
��CB=CMʱ��t=4��
���� ���⿼���˶�������ĺ���ͼ��ͬʱҪ��Ϥ���������ε��ж������ʡ����ɶ�����֪ʶ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
14���ں���y=$\sqrt{x-3}$�У��Ա���x��ȡֵ��Χ�ǣ�������
| A�� | x��3 | B�� | x��3 | C�� | x��3 | D�� | x��3 |
11��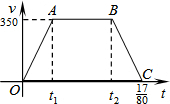 ����������·�ѿ������裬ijУ�о���ѧϰ�Դ�Ϊ���⣬���о��г�����ʻ�ٶ�ʱ���õ�һ����ѧ���⣮��ͼ����v�ǹ���t�ĺ�����ͼ��Ϊ����O-A-B-C������A��t1��350����B��t2��350����C��$\frac{17}{80}$��0�����ı���OABC�����Ϊ70����t1-t2=��������
����������·�ѿ������裬ijУ�о���ѧϰ�Դ�Ϊ���⣬���о��г�����ʻ�ٶ�ʱ���õ�һ����ѧ���⣮��ͼ����v�ǹ���t�ĺ�����ͼ��Ϊ����O-A-B-C������A��t1��350����B��t2��350����C��$\frac{17}{80}$��0�����ı���OABC�����Ϊ70����t1-t2=��������
 ����������·�ѿ������裬ijУ�о���ѧϰ�Դ�Ϊ���⣬���о��г�����ʻ�ٶ�ʱ���õ�һ����ѧ���⣮��ͼ����v�ǹ���t�ĺ�����ͼ��Ϊ����O-A-B-C������A��t1��350����B��t2��350����C��$\frac{17}{80}$��0�����ı���OABC�����Ϊ70����t1-t2=��������
����������·�ѿ������裬ijУ�о���ѧϰ�Դ�Ϊ���⣬���о��г�����ʻ�ٶ�ʱ���õ�һ����ѧ���⣮��ͼ����v�ǹ���t�ĺ�����ͼ��Ϊ����O-A-B-C������A��t1��350����B��t2��350����C��$\frac{17}{80}$��0�����ı���OABC�����Ϊ70����t1-t2=��������| A�� | $\frac{1}{5}$ | B�� | $\frac{3}{16}$ | C�� | $\frac{7}{80}$ | D�� | $\frac{31}{160}$ |
 ij�о���ѧϰС�飬Ϊ�˲���ij������A��B�����ľ��룬��һ�ܺ�ģ��ֱ��AB�����Ϸ�24�ĸ߶ȷ��У�����ģλ�ڵ�D��ʱ����A�㴦��ú�ģ����Ϊ60�㣬5���Ӻ���ģ�ڵ�C��ʱ����B���ú�ģ����Ϊ45�㣬��֪��ģ���е��ٶ�Ϊÿ����45�ף��Լ���A��B����ľ��룮�������ȷ��0.1�ף��ο����ݣ�$\sqrt{2}=1.41��\sqrt{3}$=1.73����
ij�о���ѧϰС�飬Ϊ�˲���ij������A��B�����ľ��룬��һ�ܺ�ģ��ֱ��AB�����Ϸ�24�ĸ߶ȷ��У�����ģλ�ڵ�D��ʱ����A�㴦��ú�ģ����Ϊ60�㣬5���Ӻ���ģ�ڵ�C��ʱ����B���ú�ģ����Ϊ45�㣬��֪��ģ���е��ٶ�Ϊÿ����45�ף��Լ���A��B����ľ��룮�������ȷ��0.1�ף��ο����ݣ�$\sqrt{2}=1.41��\sqrt{3}$=1.73����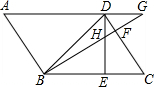 ��ͼ����֪ƽ���ı���ABCD�У���DBC=45�㣬DE��BC��E��BF��CD��F��DE��BF�ཻ��H��BF��AD���ӳ����ཻ��G��������ۣ���1��AB=BH����2����A=��BHE����3��BH=HG����4����BHD�ס�BDG����5��DB=$\sqrt{2}$BE��������ȷ�Ľ����У�1����2����5��������ţ���
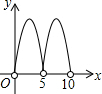
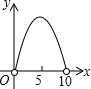
��ͼ����֪ƽ���ı���ABCD�У���DBC=45�㣬DE��BC��E��BF��CD��F��DE��BF�ཻ��H��BF��AD���ӳ����ཻ��G��������ۣ���1��AB=BH����2����A=��BHE����3��BH=HG����4����BHD�ס�BDG����5��DB=$\sqrt{2}$BE��������ȷ�Ľ����У�1����2����5��������ţ���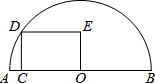 ��ͼ��C�ǰ�ԲO��ֱ��AB�ϵ�һ�����㣨����A��B�غϣ�����C��AB�Ĵ��߽���Բ�ڵ�D���Ե�D��C��OΪ����������DCOE����AB=10����AC=x������DCOE�����Ϊy��������ͼ�����ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
��ͼ��C�ǰ�ԲO��ֱ��AB�ϵ�һ�����㣨����A��B�غϣ�����C��AB�Ĵ��߽���Բ�ڵ�D���Ե�D��C��OΪ����������DCOE����AB=10����AC=x������DCOE�����Ϊy��������ͼ�����ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������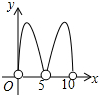
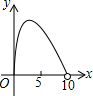
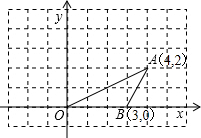 ��ͼ����O��A��B������ֱ�Ϊ��0��0������4��2������3��0��������OAB�Ƶ�O����ʱ�뷽����ת90��õ���OCD������Aת����C��
��ͼ����O��A��B������ֱ�Ϊ��0��0������4��2������3��0��������OAB�Ƶ�O����ʱ�뷽����ת90��õ���OCD������Aת����C��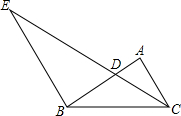 ��ͼ����DΪ��ABC�ı�AB�ϵ�һ�㣬����CD������B��BE��AC��CD���ӳ����ڵ�E���ҡ�ACD=��DBC��S��ADC��S��BED=4��9��AB=10����AC�ij�Ϊ2$\sqrt{10}$��
��ͼ����DΪ��ABC�ı�AB�ϵ�һ�㣬����CD������B��BE��AC��CD���ӳ����ڵ�E���ҡ�ACD=��DBC��S��ADC��S��BED=4��9��AB=10����AC�ij�Ϊ2$\sqrt{10}$�� �ס�����������ͬ��·����A�ص�B������ǰ����A��B���ؼ��·��Ϊ20ǧ�ף�����ǰ����·��Ϊs����λ��ǧ�ף����׳������ʱ��Ϊt����λ��Сʱ�����ס���ǰ����·����ʱ��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ�ش��������⣺
�ס�����������ͬ��·����A�ص�B������ǰ����A��B���ؼ��·��Ϊ20ǧ�ף�����ǰ����·��Ϊs����λ��ǧ�ף����׳������ʱ��Ϊt����λ��Сʱ�����ס���ǰ����·����ʱ��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ�ش��������⣺