题目内容
13．适合下列条件的△ABC中，直角三角形的个数为（ ）①∠A：∠B：∠C=1：2：3；②∠A+∠B=∠C；③∠A=90°-∠B；④∠A=∠B=2∠C．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 先根据三角形的内角和是180°对①②③④中△ABC的形状作出判断即可．
解答 解：①∵∠A：∠B：∠C=1：2：3，
∴设∠A=x，则∠B=2x，∠C=3x，
∴x+2x+3x=180°，解得x=30°，
∴∠C=3x=90°，
∴△ABC是直角三角形，故本小题正确；
②∵∠A+∠B=∠C，
∴2∠C=180°，解得∠C=90°，故本小题正确；
③∵∠A=90°-∠B，
∴∠A+∠B=90°，
∴∠C=180°-90°=90°，故本小题正确；
④∵∠A=∠B=2∠C，
∴5∠C=180°，解得∠C=36°，
∴∠A=∠B=72°，故本小题错误．
故选C．
点评 本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠BAO．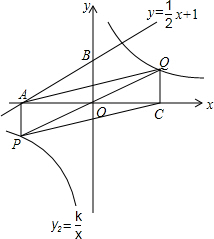
如图，已知一次函数y1=$\frac{1}{2}$x+1的图象与x轴、y轴的交点分别是A、B，反比例函数y2=$\frac{k}{x}$（k是常数，k≠0）的图象上一点P满足：①PA⊥x轴；②cos∠AOP=$\frac{2\sqrt{5}}{5}$（O为坐标原点）．
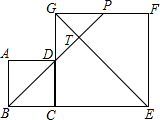如图，边长分别为3和5的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则ET的长为4$\sqrt{2}$．
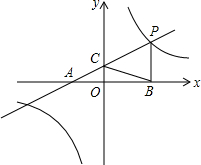如图，点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点，直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C，过P作PB垂直于x轴，若AB+PB=9，则△PBC的面积为（ ）