题目内容
7.有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ的形状,并证明.
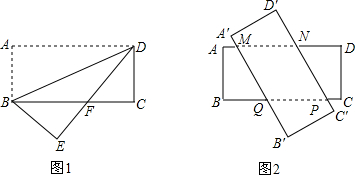
分析 (1)根据折叠的性质可得∠ADB=∠EDB,再根据两直线平行,内错角相等可得∠ADB=∠DBC,然后求出∠FBD=∠FDB,根据等角对等边可得BF=DF,设BF=x,表示出CF,在Rt△CDF中,利用勾股定理列出方程求解即可;
(2)根据MN∥PQ,MQ∥AP,所以四边形MNPQ是平行四边形,过点N分别做NE⊥MQ,NF⊥QP,垂足分别为E、F,可得NF=NE,根据S平行四边形MNPQ=NE•MQ=NF•PQ,所以MQ=PQ,所以四边形MNPQ是菱形.
解答 解:(1)由折叠得,∠ADB=∠EDB,
∵矩形ABCD的对边AD∥BC,
∴∠ADB=∠DBC,
∴∠FBD=∠FDB,
∴BF=DF,
设BF=x,则CF=8-x,
在Rt△CDF中,CD2+CF2=DF2
即32+(8-x)2=x2,
解得:x=$\frac{73}{16}$,
即BF=$\frac{73}{16}$;
(2)四边形MNPQ的形状是菱形,
证明:∵矩形纸片ABCD和A′B′C′D′,
∴MN∥PQ,MQ∥AP,
∴四边形MNPQ是平行四边形,①
如图2,
过点N分别做NE⊥MQ,NF⊥QP,垂足分别为E、F,
∴NF=NE,
∵S平行四边形MNPQ=NE•MQ=NF•PQ,
∴MQ=PQ,②
由①②知,四边形MNPQ是菱形.
点评 本题考查了翻折变换的性质,矩形的性质,勾股定理的应用,菱形的判定与性质,熟记翻折的性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
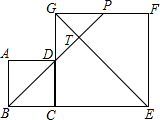 如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.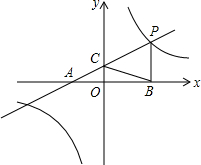 如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )
如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )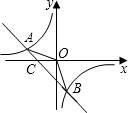 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$的图象的两个交点.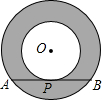 如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )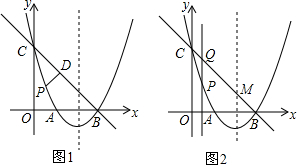
 在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm.
在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm.