题目内容
2.设直线y=-$\frac{n}{n+1}$x+$\frac{{\sqrt{2}}}{n+1}$(n为正整数)与两坐标轴围成的三角形面积为Sn(n=1,2,…,2012),则S1+S2+…+S2012的值为$\frac{2012}{2013}$.分析 依次求出S1、S2、Sn,就发现规律:Sn=$\frac{1}{n(n+1)}$,然后求其和即可求得答案.注意$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
解答 解:∵当n=1时,y=-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$,此时,A(0,$\frac{\sqrt{2}}{2}$),B($\sqrt{2}$,0),
∴S1=$\frac{1}{2}$×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{1×2}$;
同理可得,S2=$\overline{\frac{1}{2}}$×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{3}$=$\frac{1}{2×3}$,
…,
∴Sn=$\frac{1}{n(n+1)}$,
∴S1+S2+S3+…+S2012=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2012×2013}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$
=1-$\frac{1}{2013}$
=$\frac{2012}{2013}$.
故答案为:$\frac{2012}{2013}$.
点评 此题考查了一次函数图象上点的坐标特征,根据题意找出规律是解答此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7.用火柴棒按下图中的方式搭图形.

①按图示规律填空.
②按照这种方式搭下去,搭第n个图形需要4n+1根火柴棒(写最简答案),共有2n个三角形.

①按图示规律填空.
| 图形标号 | (1) | (2) | (3) | (4) |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
| 三角形个数 | 2 | 4 | 6 | 8 |
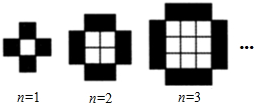 当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).
当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数). 如图,函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1>y2时,x的范围是x<-1,x>2.
如图,函数y1=|x|,y2=$\frac{1}{3}$x+$\frac{4}{3}$.当y1>y2时,x的范围是x<-1,x>2.