题目内容
已知△ABC中，AB=AC，D是∠BAC的平分线上一点，则△DBC是什么三角形？试说明理由．
考点：全等三角形的判定与性质,等腰三角形的性质
专题：计算题
分析：△DBC为等腰三角形，理由为：由AE为等腰三角形顶角平分线，得到一对角相等，再由AB=AC，AD为公共边，利用SAS得到三角形ABD与三角形ACD全等，利用全等三角形对应边相等得到BD=CD，得证．
解答：
解：△DBC为等腰三角形，理由为：
∵AE为∠BAC的平分线，
∴∠BAE=∠CAE，
在△ABD和△ACD中，
，
∴△ABD≌△ACD（SAS），
∴BD=CD，
则△BDC为等腰三角形．
解：△DBC为等腰三角形，理由为：∵AE为∠BAC的平分线，
∴∠BAE=∠CAE，
在△ABD和△ACD中，
|
∴△ABD≌△ACD（SAS），
∴BD=CD，
则△BDC为等腰三角形．
点评：此题考查了全等三角形的性质与判定，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
相关题目
若
，则用只含x的代数式表示为（ ）
|
| A、y=2x+7 |
| B、y=7-2x |
| C、y=-2x-5 |
| D、y=2x-5 |
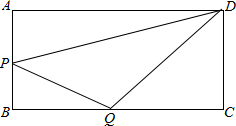在矩形ABCD中，AB=5，BC=12，点P从点B开始沿AB向点A以1个单位每秒的速度移动，点Q从点B开始沿BC边向点C以2个单位每秒的速度移动，点P到点A或点Q到点C停止移动，如果P、Q分别从B同时出发，连接PQ、DQ、DP，问几秒钟时△DPQ的面积是8？
如图，Rt△ABC中，延长斜边中线CD到E，使CD=DE，连接AE，BE，则四边形AEBC是什么图形，说明理由．
如图，∠C=∠CAM=90°，AC=8，BC=4，P、Q两点分别在线段AC和射线AM上运动，且PQ=AB．当AP=