题目内容
16.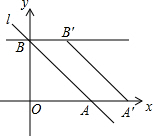 如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4.
如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4.(1)求B点坐标;
(2)在y轴上是否存在点P,使得S△ABP=$\frac{1}{2}$S△AOP?若存在,求出P点坐标;若不存在,请说明理由.
分析 (1)利用平移的性质可判定四边形ABB′A′为平行四边形,则根据平行四边形的面积公式可计算出OB=2,所以B(0,2);
(2)设P(0,t),根据三角形面积公式得到$\frac{1}{2}$•4•|2-t|=$\frac{1}{2}$•$\frac{1}{2}$•4•|t|,然后解绝对值方程求出t,即可得到P点坐标.
解答 解:(1)∵线段AB沿x轴正方向平移2个单位长度至A′B′,
∴四边形ABB′A′为平行四边形,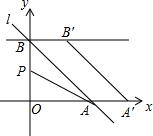
∴OB•2=4,
解得OB=2,
∴B(0,2);
(2)存在.
设P(0,t),
∵S△ABP=$\frac{1}{2}$S△AOP,
∴$\frac{1}{2}$•4•|2-t|=$\frac{1}{2}$•$\frac{1}{2}$•4•|t|,
解得t=$\frac{4}{3}$或t=4,
∴P点坐标为(0,$\frac{4}{3}$),(0,4).
点评 本题考查了一次函数图象与几何变换:一次函数y=kx+b向上平移m(m>0)个单位后所得直线解析式为y=kx+b+m,向下平移m(m>0)个单位后所得直线解析式为y=kx+b-m.也考查了三角形面积公式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
14. 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2015的坐标是( )| A. | (22014,22014) | B. | (22015,22015) | C. | (22014,22015) | D. | (22015,22014) |
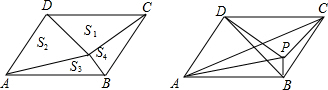
11. 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )
 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
6.在?ABCD中,∠BAD的角平分线交BC于点E,且AE=BE,则∠BCD的度数为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |