题目内容
11. 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
分析 求出BE=DE,由勾股定理得出BD2=DE2+BE2,即可判断①;求出∠DHF=∠C,根据平行四边形的性质得出AB=CD,∠A=∠C,即可判断②;证△BHE≌△DCE,推出BH=DC,根据AB=CD即可判断③.
解答 解:∵DE⊥BC,
∴∠DEB=90°,
∵∠DBC=45°,
∴∠BDE=45°=∠DBE,
∴BE=DE,
由勾股定理得:BD2=DE2+BE2,
即BD=$\sqrt{2}$DE,∴①正确;
∵DE⊥BC,BF⊥CD,
∴∠DEC=∠HFD=90°,
∴∠DHF+∠EDC=90°,∠EDC+∠C=90°,
∴∠DHF=∠C,
∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,
∵∠DHF=∠BHE,
∴∠A=∠BHE,∴②正确;
在△BHE和△DCE中
$\left\{\begin{array}{l}{∠HBE=∠EDC}\\{BE=DE}\\{∠BEH=∠DEC}\end{array}\right.$,
∴△BHE≌△DCE,
∴BH=DC,
∵AB=CD,
∴BH=AB,∴③正确;
故选A
点评 本题考查了平行四边形的性质等腰三角形的性质,全等三角形的性质和判定,勾股定理的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,有一定的难度.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | a2•a3=a5 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a3÷a2=1 |
2.对有理数a、b,有如下的判断:其中正确的个数( )
(1)若|a|=|b|,则a=b.
(2)若a=-b,则(-a)2=b2
(3)若|a|>b,则|a|>|b|
(4)若|a|<|b|,则a<b.
(1)若|a|=|b|,则a=b.
(2)若a=-b,则(-a)2=b2
(3)若|a|>b,则|a|>|b|
(4)若|a|<|b|,则a<b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.2008年下半年金融风暴席卷全球,我市某厂从2009年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下:
请你认真分析表中数据,从你所学习过的一次函数和反比例函数中确定哪种函数能表示其变化规律?说明确定是这种函数而不是另一种函数的理由,并求出它的关系式.
| 月 份 | 1 | 2 | 3 | 4 |
| 投入技术改进资金x/万元 | 2.5 | 3 | 4 | 4.5 |
| 产品成本y/(万元/件) | 7.2 | 6 | 4.5 | 4 |

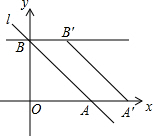 如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4.
如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4.