题目内容
4.已知平行四边形ABCD的面积为60cm2,点P是其内部一点,连接PA,PB,PC,PD,将平行四边形分成四个三角形,其面积分别记为如图所示的S1、S2、S3、S4.如果过P点分别做上述四个三角形的高,你会发现S1、S2、S3、S4满足S1+S3=S2+S4,请应用这个结论解决下列问题: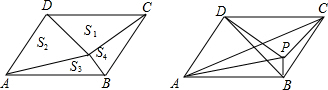
(1)若S2=2S1,S3=3S4,求S1+S2的值.
(2)在(1)的条件下,连接AC、BD,求三角形PBD与三角形PAC的面积和.
分析 (1)过点P分别作PF⊥AD于点F,PE⊥AB于点E,由于△APD以AD为底边,△PBC以BC为底边,得到此时两三角形的高的和为AD与BC的距离,根据三角形面积的求法得到S2+S4=$\frac{1}{2}$S四边形ABCD=30,同理可得出S1+S3=$\frac{1}{2}$S四边形ABCD=30,然后根据数量之间的关系即可得到结果;
(2)由(1)知S1=12,S2=24,求得S3=30-12=18,S4=30-24=6,然后根据各图形之间的关系即可得到结果.
解答  解:(1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
解:(1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AD与BC的距离,∴S2+S4=$\frac{1}{2}$S四边形ABCD=30,
同理可得出S1+S3=$\frac{1}{2}$S四边形ABCD=30,
∴S2=$\frac{1}{2}$S四边形ABCD-S4=30-S4,
∵S2=2S1,S3=3S4,
∴S1+S3=S1+3S4=S1+3(30-S2)=S1+3(30-2S1)=30,
∴S1=12,
∴S2=24,
∴S1+S2=36;
(2)由(1)知S1=12,S2=24,
∴S3=30-12=18,S4=30-24=6,
∴S△PBD+S△PAC
=S△BDC-S1-S4+S△ABC-S3-S4
=$\frac{1}{2}$S四边形ABCD-S1-S4+$\frac{1}{2}$四边形ABCD-S3-S4
=18.
点评 本题主要考查了平行四边形的性质以及三角形面积求法,正确的识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知有理数a、b、c在数轴的对应位置如图,则|a-1|+|a-c|+|a-b|可化简为1-c-a+b.
已知有理数a、b、c在数轴的对应位置如图,则|a-1|+|a-c|+|a-b|可化简为1-c-a+b.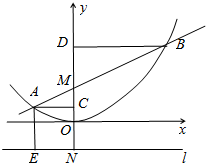 如图所示,过y轴上一点M(0,1)作直线与二次函数y=$\frac{1}{4}$x2的图象交于A、B两点,过A、B两点分别作y轴的垂线,垂足为C、D,直线l过点M关于原点O的对称点N,且与y轴垂直.过点A作l的垂线,垂足为E.
如图所示,过y轴上一点M(0,1)作直线与二次函数y=$\frac{1}{4}$x2的图象交于A、B两点,过A、B两点分别作y轴的垂线,垂足为C、D,直线l过点M关于原点O的对称点N,且与y轴垂直.过点A作l的垂线,垂足为E.
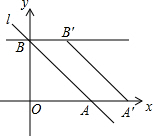 如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4.
如图,在平面直角坐标系中,直线l分别与x轴、y轴交于A(4,0)、B两点,将线段AB沿x轴正方向平移2个单位长度至A′B′,AB扫过的面积为S四边形ABB′A′=4. 把长方形纸片ABCD沿对角线AC折叠,得到如图所示的图形,AD平分∠B′AC,则∠B′CD=30°.
把长方形纸片ABCD沿对角线AC折叠,得到如图所示的图形,AD平分∠B′AC,则∠B′CD=30°.