题目内容
8. 如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.
如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.(1)求点A的坐标及直线l2的解析式;
(2)求△ABD的面积;
(3)是否存在点M,使A、B、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
分析 (1)在y=2x-2中,令y=0,即可求得横坐标,则A的坐标即可求得;
(2)利用待定系数法即可求得直线AC的解析式;
(3)首先解方程组求得D的坐标,然后利用图象的平移,M可以看成由A或B或D平移得到,利用平移方向、距离与坐标变化之间的关系即可求得.
解答 解:(1)在y=2x-2中,令y=0,则2x-2=0,解得x=1,
则A的坐标是(1,0).
设直线l2的解析式是y=kx+b,
则$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
则直线l2的解析式是y=-x+4;
(2)根据题意得:$\left\{\begin{array}{l}{y=2x-2}\\{y=-x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
AB=4-1=3,
则S△ABD=$\frac{1}{2}$×3×2=3;
(3)当四边形ABMD是平行四边形时,A的坐标是(1,0),D的坐标是(2,2),即A向右平移一个单位长度,向上移动2个单位长度得到D,则M的坐标是(4+1,0+2),即(5,2);
当四边形ABDM是平行四边形时,B到D是向左平移2个单位长度,再向上平移2个单位长度,则M的坐标是(-1,2);
当四边形AMBD是平行四边形时,D到A是向左平移1个单位长度,然后向下平移2个单位长度,则M的坐标是(3,-2).
总之,M的坐标是(5,1)或(-1,2)或(3,-2).
点评 本题考查了待定系数法求函数的解析式以及平行四边形的性质,理解M可以看成由A或B或D平移得到是关键.

| A. | 0.25×10-2 | B. | 2.5×10-3 | C. | 2.5×10-2 | D. | 2.5×104 |
| A. | 2m+3n=5mn | B. | a6÷a2=a4 | C. | (a2)3=a6 | D. | a•a2=a3 |
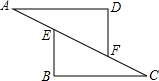 如图,已知点A、E、F、C在同一直线上,AE=FC,过点A、C 作AD∥BC,且AD=CB.
如图,已知点A、E、F、C在同一直线上,AE=FC,过点A、C 作AD∥BC,且AD=CB.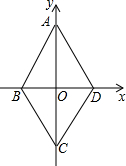 如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0).
如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0).
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
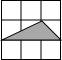
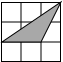
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2. 如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )
如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )

 如图,在Rt△ABC中,∠C=90°,∠A=40°,则∠B=50°.
如图,在Rt△ABC中,∠C=90°,∠A=40°,则∠B=50°.