题目内容
10.如果要使(x+1)(x2-2ax+a2)的乘积中不含x2项,则a=$\frac{1}{2}$.分析 先根据多项式的乘法法则展开,再根据题意,二次项的系数等于0列式求解即可.
解答 解:原式=x3-2ax2+a2x+x2-2ax+a2
=x3+(1-2a)x2+a2x+a2,
∵乘积中不含x2项,
∴1-2a=0,
解得:a=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查多项式与多项式的乘法,运算法则需要熟练掌握,不含某一项就让这一项的系数等于0是解题的关键.

练习册系列答案
相关题目
2.将一个正方体沿某些棱展开后,能够得到的平面图形是( )
| A. |  | B. |  | C. |  | D. |  |
18. a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )
 a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )| A. | -a-b | B. | a+b | C. | a-b | D. | b-a |
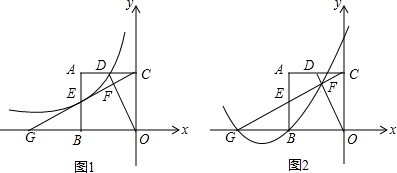
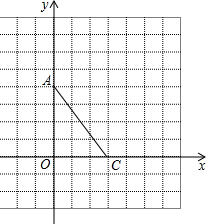 如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.
如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.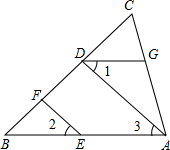 如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.
如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.