题目内容
4.已知x是$\sqrt{5}$的小数部分,则$\frac{{x}^{2}}{{x}^{2}-1}÷(\frac{1}{x-1}+1)$=$\frac{3-\sqrt{5}}{4}$.分析 将分母因式分解,计算括号内分式加法,再将除法转化为乘法,最后约分可化简原式,将x的值代入计算即可.
解答 解:原式=$\frac{{x}^{2}}{(x+1)(x-1)}$÷$\frac{x}{x-1}$
=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x}$
=$\frac{x}{x+1}$,
∵x是$\sqrt{5}$的小数部分,且2<$\sqrt{5}$<3,
∴x=$\sqrt{5}$-2,
∴原式=$\frac{\sqrt{5}-2}{\sqrt{5}-1}$
=$\frac{(\sqrt{5}-2)(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}$
=$\frac{3-\sqrt{5}}{4}$.
故答案为:$\frac{3-\sqrt{5}}{4}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的基本性质和分式的运算法则是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.下列各组线段中,不能够组成直角三角形的一组是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 2,3,4 |
 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )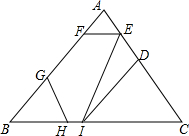 如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB.
如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB. 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=6,则四边形CODE的周长为12.
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=6,则四边形CODE的周长为12.