题目内容
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO.抛物线y=ax2-5ax+4经过△ABC的三个顶点.
(1)求抛物线的解析式;
(2)正方形EFGH的顶点E在线段AB上,顶点F在对称轴右侧的抛物线上,边GH在x轴上,求正方形EFGH的边长;
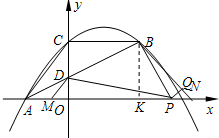
(3)设直线AB与y轴的交点为D,在x轴上是否存在点P,使∠DPB=45°?若存在,求出点P的坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)正方形EFGH的顶点E在线段AB上,顶点F在对称轴右侧的抛物线上,边GH在x轴上,求正方形EFGH的边长;
(3)设直线AB与y轴的交点为D,在x轴上是否存在点P,使∠DPB=45°?若存在,求出点P的坐标;若不存在,请说明理由.

考点:二次函数综合题
专题:压轴题
分析:(1)根据已知抛物线,利用对称轴公式代入数据即可得出对称轴,同时也可以得出C点的坐标,利用AC=BC,即可得出A点的坐标和B点的坐标,代入抛物线方程即可得出a的值,即得出该抛物线的解析式;
(2)设正方形的边长为m(m>0),首先利用待定系数法求得直线AB的解析式,然后即可求得正方形的边长;
(3)作BK⊥x轴于K,再取M(-
,0)和N(9,0),根据△DOP∽△PQB 即可求得点P的坐标.
(2)设正方形的边长为m(m>0),首先利用待定系数法求得直线AB的解析式,然后即可求得正方形的边长;
(3)作BK⊥x轴于K,再取M(-
| 3 |
| 2 |
解答:解:(1)∵抛物线y=ax2-5ax+4经过△ABC的三个顶点,
∴当x=0时,y=4,
∴C(0,4),且抛物线的对称轴是直线x=-
=
,
∴B(5,4),
∵BC∥x轴,AB平分∠CAO,
∴∠CAB=∠BAO,∠BAO=∠ABC,
∴∠CAB=∠ABC,
∴AC=BC=5,
∴AO=
=3,
即A(-3,0),
∴9a+15a+4=0,
解得a=-
∴抛物线的解析式是y=-
x2+
x+4;
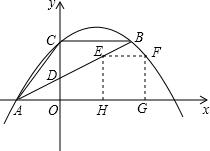 (2)不妨设正方形的边长为m(m>0),
(2)不妨设正方形的边长为m(m>0),
设直线AB的解析式为:y=kx+b,
,
解得:
,
∴直线AB的解析式为:y=
x+
,
当y=m时,x=2m-3,
∴点E(2m-3,m),
∴点F(3m-3,m)
代入抛物线得:-
(3m-3)2+
(3m-3)+4=m,
即3m2-9m=0,
解得:m=0或3;
 ∴正方形EFGH的边长为3.
∴正方形EFGH的边长为3.
(3)作BK⊥x轴于K,再取M(-
,0)和N(9,0)
只有当点P落在M、O之间和K、N之间各一个位置能使∠DPB=45°,
如图,当点P在KN上时,再作PQ⊥BN于Q,可证△DOP∽△PQB 有
=
,
先求出D(0,
),再设P(x,0),
∴
(4
-
)=x•
经整理得,2x2-15x-3=0,解得x=
,应取x=
…(8分)
同理,当当点P在AO上时,4(
-
,
))=
,
)(5-x),
经整理得,2x2-15x-3=0,解得x=
,应取x=
…(10分)
综上所述,在x轴上存在符合要求的两点P(
,0).
∴当x=0时,y=4,
∴C(0,4),且抛物线的对称轴是直线x=-
| -5a |
| 2a |
| 5 |
| 2 |
∴B(5,4),
∵BC∥x轴,AB平分∠CAO,
∴∠CAB=∠BAO,∠BAO=∠ABC,
∴∠CAB=∠ABC,
∴AC=BC=5,
∴AO=
| AC2-OC2 |
即A(-3,0),
∴9a+15a+4=0,
解得a=-
| 1 |
| 6 |
∴抛物线的解析式是y=-
| 1 |
| 6 |
| 5 |
| 6 |
 (2)不妨设正方形的边长为m(m>0),
(2)不妨设正方形的边长为m(m>0),设直线AB的解析式为:y=kx+b,
|
解得:
|
∴直线AB的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
当y=m时,x=2m-3,
∴点E(2m-3,m),
∴点F(3m-3,m)
代入抛物线得:-
| 1 |
| 6 |
| 5 |
| 6 |
即3m2-9m=0,
解得:m=0或3;
 ∴正方形EFGH的边长为3.
∴正方形EFGH的边长为3.(3)作BK⊥x轴于K,再取M(-
| 3 |
| 2 |
只有当点P落在M、O之间和K、N之间各一个位置能使∠DPB=45°,
如图,当点P在KN上时,再作PQ⊥BN于Q,可证△DOP∽△PQB 有
| DO |
| OP |
| PQ |
| QB |
先求出D(0,
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 2 |
| 9-x | ||
|
| 9-x | ||
|
经整理得,2x2-15x-3=0,解得x=
15±
| ||
| 4 |
15+
| ||
| 4 |
同理,当当点P在AO上时,4(
3
| ||
| 2 |
| x+\f(3 |
| 2 |
| 2 |
| x+\f(3 |
| 2 |
| 2 |
经整理得,2x2-15x-3=0,解得x=
15±
| ||
| 4 |
15-
| ||
| 4 |
综上所述,在x轴上存在符合要求的两点P(
15±
| ||
| 4 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知AB为⊙O的弦,弦AB=16,弓形高CD=4,则⊙O的半径长为( )
如图,已知AB为⊙O的弦,弦AB=16,弓形高CD=4,则⊙O的半径长为( )| A、12 | B、10 | C、8 | D、6 |
下列各数中属于正整数的是( )
| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
抛物线y=ax2-2x-a+1的对称轴是直线x=1,则a的值是( )
| A、-2 | B、2 | C、-1 | D、1 |
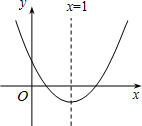 二次函数y=ax2+bx+c的图象,如图所示,其对称轴为直线x=1,若点A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象,如图所示,其对称轴为直线x=1,若点A(-1,y1),B(2,y2)是它图象上的两点,则y1与y2的大小关系是( )| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、不能确定 |
 如图,△ABC内接于⊙O,P为⊙O上一点,且∠APC=∠BPC,则△ABC的形状为( )
如图,△ABC内接于⊙O,P为⊙O上一点,且∠APC=∠BPC,则△ABC的形状为( )| A、等腰三角形 |
| B、等边三角形 |
| C、任意三角形 |
| D、△ABC的形状由P点的位置决定 |