题目内容
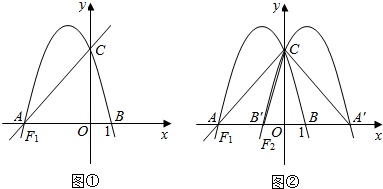
5. 对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.
对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.(1)分别判断函数y=x-1,y=$\frac{1}{x}$,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx.
①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3)记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2.函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为.
分析 (1)根据定义分别求解即可求得答案;
(2)①首先由函数y=2x2-bx=x,求得x(2x-b-1)=0,然后由其不变长度为零,求得答案;
②由①,利用1≤b≤3,可求得其不变长度q的取值范围;
(3)由记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,可得函数G的图象关于x=m对称,然后根据定义分别求得函数的不变值,再分类讨论即可求得答案.
解答 解:(1)∵函数y=x-1,令y=x,则x-1=x,无解;
∴函数y=x-1没有不变值;
∵函数y=$\frac{1}{x}$,令y=x,则x=$\frac{1}{x}$,解得:x=±1,
∴函数y=$\frac{1}{x}$的不变值为±1,q=1-(-1)=2,
∵函数y=x2,令y=x,则x=x2,解得:x1=0,x2=1,
∴函数y=x2的不变值为:0或1,q=1-0=1;
(2)①函数y=2x2-bx,令y=x,则x=2x2-bx,
整理得:x(2x-b-1)=0,
∵q=0,
∴x=0且2x-b-1=0,
解得:b=-1;
②由①知:x(2x-b-1)=0,
∴x=0或2x-b-1=0,
解得:x1=0,x2=$\frac{b+1}{2}$,
∵1≤b≤3,
∴1≤x2≤2,
∴1-0≤q≤2-0,
∴1≤q≤2;
(3)∵记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2.
∴函数G的图象关于x=m对称,
∴G:y=$\left\{\begin{array}{l}{{x}^{2}-2x(x≥m)}\\{(2m-x)^{2}-2(2m-x)(x<m)}\end{array}\right.$,
∵当x2-2x=x时,x3=0,x4=3;
当(2m-x)2-2(2m-x)=x时,△=1+8m,
当△<0,即m<-$\frac{1}{8}$时,q=x4-x3=3;
当△≥0,即m≥-$\frac{1}{8}$时,x5=$\frac{4m-1+\sqrt{1+8m}}{2}$,x6=$\frac{4m-1-\sqrt{1+8m}}{2}$,
①当-$\frac{1}{8}$≤m≤0时,x3=0,x4=3,
∴x6<0,
∴x4-x6>3(不符合题意,舍去);
②∵当x5=x4时,m=1,当x6=x3时,m=3;
当0<m<1时,x3=0(舍去),x4=3,
此时0<x5<x4,x6<0,q=x4-x6>3(舍去);
当1≤m≤3时,x3=0(舍去),x4=3,
此时0<x5<x4,x6>0,q=x4-x6<3;
当m>3时,x3=0(舍去),x4=3(舍去),
此时x5>3,x6<0,q=x5-x6>3(舍去);
综上所述:m的取值范围为1≤m≤3或m<-$\frac{1}{8}$.
点评 此题属于二次函数的综合题,考查了二次函数、反比例函数、一次函数的性质以及函数的对称性.注意掌握分类讨论思想的应用是解此题的关键.

| A. | a2+a3=2a5 | B. | a2•a3=a6 | C. | (a2)3=a8 | D. | a4÷a3=a |
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
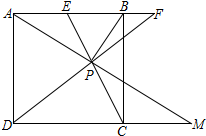 如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F
如图,点P为正方形ABCD内一点,且∠APB=90°,延长AP交直线CD于M,分别延长CP、DP交直线AB于点E、F