题目内容
现有一个长和宽的比为4：3的长方形，此长方形的周长为14
cm，则此长方形的面积为 ．
| 3 |
考点：二次根式的应用
专题：
分析：首先利用矩形的长与宽的比值结合其周长得出长与宽，进而求出面积．
解答：解：∵一个长和宽的比为4：3的长方形，
∴设长方形的长为4x，宽为3x，则2（4x+3x）=14
，
解得：x=
，则长为4
cm，宽为3
cm，
故此长方形的面积为：4
×3
=36（cm2）．
故答案为：36cm2．
∴设长方形的长为4x，宽为3x，则2（4x+3x）=14
| 3 |
解得：x=
| 3 |
| 3 |
| 3 |
故此长方形的面积为：4
| 3 |
| 3 |
故答案为：36cm2．
点评：此题主要考查了二次根式的应用，得出长方形的长与宽是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
下列长度的三条线段，能组成三角形的是（ ）
| A、1cm，3cm，2cm |
| B、5cm，5cm，20cm |
| C、5cm，6cm，10cm |
| D、5cm，20cm，10cm |
如图所示，在△ABC中，CD⊥AB于点D，若AB=5，CD=2在Rt△ABC中，∠C=90°，sinA=
，则cosB的值为（ ）
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在一块长为am，宽为bm的长方形草地上，有一条弯曲的小路，小路左边线向右平移1m就是它的右边线，求这块草地的绿地面积．
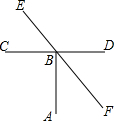如图，AB⊥CD于B，EF是经过B点的一条直线，若∠EBD=135°，则∠ABF=（ ）| A、30° | B、45° |
| C、60° | D、75° |
已知抛物线y=-