题目内容
 已知抛物线y=-
已知抛物线y=-| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:二次函数图象与几何变换
专题:计算题
分析:设E(x1,y1),(x2,y2),利用勾股定理和两点间的距离公式得到x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,整理得到x1x2+y1y2=0,再根据一次函数图象的平移问题得到直线y=
x向下平移n个单位后的解析式为y=
x+n,则根据二次函数图象与异次函数图象的交点问题得到
,消去y得-
x2+
x=
x+n,整理得2x2+x+6n=0,利用根与系数的关系得到x1+x2=-
,x1x2=3n,接着用n表示y1y2,然后利用x1x2+y1y2=0得到关于n的一元二次方程,再解方程即可得到n的值.
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设E(x1,y1),(x2,y2),
∵∠EOF=90°,
∴OE2+OF2=EF2,
∴x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,
∴x1x2+y1y2=0,
直线y=
x向下平移n个单位后的解析式为y=
x+n,
由方程组
得-
x2+
x=
x+n,
整理得2x2+x+6n=0,
∴x1+x2=-
,x1x2=3n,
∵y1y2=(
x1+n)(
x2+n)=
x1x2+
n(x1+x2)+n2=
•3n-
n•
+n2=n2+
n,
∴3n+n2+
n=0,解得n1=0(舍去),n2=-
,
∴n的值为-
.
∵∠EOF=90°,
∴OE2+OF2=EF2,
∴x12+y12+x22+y22=(x2-x1)2+(y2-y1)2,
∴x1x2+y1y2=0,
直线y=
| 1 |
| 2 |
| 1 |
| 2 |
由方程组
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
整理得2x2+x+6n=0,
∴x1+x2=-
| 1 |
| 2 |
∵y1y2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴3n+n2+
| 1 |
| 2 |
| 7 |
| 2 |
∴n的值为-
| 7 |
| 2 |
点评:本题考查了一次函数图象与几何变换:一次函数y=kx+b向下平移m个单位所得直线解析式为y=kx+b-m.也考查了勾股定理和根与系数的关系、二次函数图象与二次函数图象的交点问题.

练习册系列答案
相关题目
 如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )| A、A点 | B、B点 | C、C点 | D、D点 |
下列计算正确的是( )
A、1-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
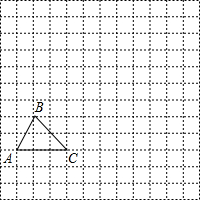 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点). 如图,圆锥的底面半径长1cm,母线AB长为4cm,动点P从B点出发,沿着圆锥体的侧面移动到AC的中点M的最短距离是多少?
如图,圆锥的底面半径长1cm,母线AB长为4cm,动点P从B点出发,沿着圆锥体的侧面移动到AC的中点M的最短距离是多少? 如图,点D是△ABC的边BC上一点,如果AB=AD=2,AC=4,且BD:DC=2:3,求证:△ABC是直角三角形.
如图,点D是△ABC的边BC上一点,如果AB=AD=2,AC=4,且BD:DC=2:3,求证:△ABC是直角三角形.