题目内容
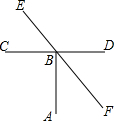如图，AB⊥CD于B，EF是经过B点的一条直线，若∠EBD=135°，则∠ABF=（ ）| A、30° | B、45° |
| C、60° | D、75° |
考点：垂线,对顶角、邻补角
专题：
分析：根据邻补角，可得∠CBE的度数，根据对顶角的性质，可得∠FBD的度数，根据余角的定义，可得答案．
解答：解：由邻补角互补，得
∠CBE=180°-∠EBD=180°-135°=45°，
由对顶角相等，得
∠DBF=∠CBE=45°，
由垂线的定义，得∠ABD=90°
由于角的定义，得
∠ABF=90°-∠DBF=90°-45°=45°，
故选：B．
∠CBE=180°-∠EBD=180°-135°=45°，
由对顶角相等，得
∠DBF=∠CBE=45°，
由垂线的定义，得∠ABD=90°
由于角的定义，得
∠ABF=90°-∠DBF=90°-45°=45°，
故选：B．
点评：本题考查了垂线，利用了对顶角邻补角，垂线的定义，余角的定义．
练习册系列答案
阅读快车系列答案
相关题目
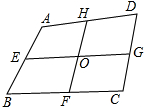在四边形ABCD中，点E，F，G，H，分别是AB，BC，CD，DE的中点，EG与FH相交于O点．
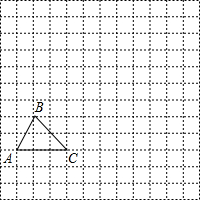如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
如图，点D是△ABC的边BC上一点，如果AB=AD=2，AC=4，且BD：DC=2：3，求证：△ABC是直角三角形．