题目内容
18.(1)计算:|-3|+$\sqrt{3}$•tan30°-$\root{3}{8}$-(2016-π)0+(-$\frac{1}{3}$)-2(2)解不等式组$\left\{\begin{array}{l}{3(x-4)+2≤5}\\{2x-3>1}\end{array}\right.$,并把其解集在数轴上表示出来.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用特殊角的三角函数值计算,第三项利用立方根定义计算,第四项利用零指数幂法则计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分求出不等式组的解集,表示在数轴上即可.
解答 解:(1)原式=3+$\sqrt{3}$×$\frac{\sqrt{3}}{3}$-2-1+9=3+1-3+9=10;
(2)$\left\{\begin{array}{l}{3(x-4)+2≤5①}\\{2x-3>1②}\end{array}\right.$,
由①得:x≤5,
由②得:x>2,
则不等式组的解集为2<x≤5.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.某市继续加大对教育经费的投入,2014年投入2500万元,2016年预计投入4000万元,假设该市投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 2500x2=4000 | B. | 2500(1+x%)2=4000 | ||
| C. | 2500(1+x)2=4000 | D. | 2500(1+x)+2500(1+x)2=4000 |
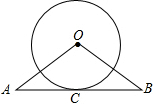 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,则OA的长为10.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,则OA的长为10.