题目内容
8.解不等式(组),并把解集表示在数轴上.(1)$\frac{2x-1}{3}$≤$\frac{3x+2}{4}$-1
(2)$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(2)据不等式的性质求出不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:(1)去分母得,4(2x-1)≤3(3x+2)-12,
去括号得,8x-4≤9x+6-12
移项得,8x-9x≤6+4-12
合并同类项得,-x≤-2
系数化为1得,x≥2,
在数轴上表示不等式的解集是: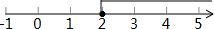 .
.
(2)$\left\{\begin{array}{l}{4x>2x-6①}\\{\frac{x-1}{3}≤\frac{x+1}{9}②}\end{array}\right.$
由①得:x>-3,
由②得:x≤2,
∴不等式组的解集是-3<x≤2.
在数轴上表示不等式组的解集是: .
.
点评 本题主要考查对解一元一次不等式(组),不等式的性质,在数轴上表示不等式的解集等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
16.下列命题中,原命题与其逆命题均为真命题的是( )
| A. | 同位角相等 | B. | 全等三角形的对应角相等 | ||
| C. | 若a=b,则|a|=|b| | D. | 等腰三角形的两底角相等 |
3.据天津市统计局统计,2014年国庆黄金周七天长假,全市共接待游客755.52万人次,将755.52万用科学记数法表示应为( )人次.
| A. | 7.5552×102 | B. | 7.5552×103 | C. | 7.5552×106 | D. | 7.5552×107 |
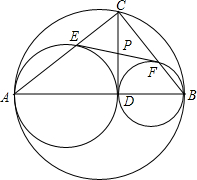 从圆上一点C向直径AB作垂线CD,D是垂足,以AD、DB为直径在大圆内分别作两个小圆,设这两个小圆的外公切线为EF,而E、F为切点,求证:CD=EF.
从圆上一点C向直径AB作垂线CD,D是垂足,以AD、DB为直径在大圆内分别作两个小圆,设这两个小圆的外公切线为EF,而E、F为切点,求证:CD=EF.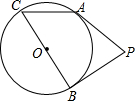 如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.
如图,点P在⊙O外,PA、PB是⊙O的切线,A、B是切点,BC是直径,若∠APB=70°,则∠ACB的度数为55°.