题目内容
13.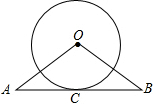 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,则OA的长为10.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,则OA的长为10.
分析 连接OC,根据切线的性质得出OC⊥AB,求出AC,根据勾股定理求出即可.
解答 解: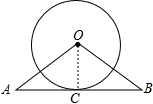
连接OC,
∵AB与⊙O相切于点C,
∴OC⊥AB,
∴∠ACO=90°,
∵∠A=∠B,
∴OA=OB,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}×$16=8,
∵OC=6,
∴由勾股定理得:OA=$\sqrt{O{C}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
故答案为:10.
点评 本题考查了切线的性质,等腰三角形的性质和判定,勾股定理的应用,能根据切线的性质求出OC⊥AB是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
3.据天津市统计局统计,2014年国庆黄金周七天长假,全市共接待游客755.52万人次,将755.52万用科学记数法表示应为( )人次.
| A. | 7.5552×102 | B. | 7.5552×103 | C. | 7.5552×106 | D. | 7.5552×107 |
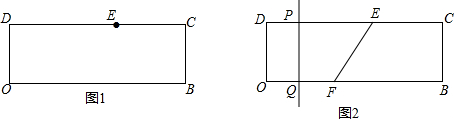
 如图,在?ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G.
如图,在?ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGC,点A的对应点为点C,点D的对应点为点G.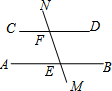 如图,MN分别交AB、CD于点E、F,AB∥CD,∠AEN=80°,则∠DFN为100°.
如图,MN分别交AB、CD于点E、F,AB∥CD,∠AEN=80°,则∠DFN为100°.