题目内容
17.计算:(1)$\frac{a-1}{{{a^2}-4a+4}}÷\frac{{{a^2}-1}}{{{a^2}-4}}$;
(2)$\frac{2a}{{{a^2}-4}}-\frac{1}{a-2}$;
(3)$\frac{{{x^2}+1}}{x-2}-\frac{3-4x}{2-x}$
(4)$({\frac{1}{{{x^2}-2x}}-\frac{1}{{{x^2}-4x+4}}})÷\frac{2}{{{x^2}-2x}}$.
分析 (1)首先把分子分母分解因式,然后把除法变成乘法,再约分后相乘即可;
(2)首先把分子分母分解因式,然后再通分后计算;
(3)首先通分,然后再根据同分母的加法进行计算,注意结果要化简;
(4)首先把分子分母分解因式,然后再先计算括号里面的减法,最后计算除法即可.
解答 解:(1)原式=$\frac{a-1}{(a-2)^{2}}$•$\frac{(a+2)(a-2)}{(a-1)(a+1)}$,
=$\frac{a+2}{(a-2)(a+1)}$;
(2)原式=$\frac{2a}{(a+2)(a-2)}$-$\frac{1}{a-2}$,
=$\frac{2a}{(a+2)(a-2)}$-$\frac{a+2}{(a+2)(a-2)}$,
=$\frac{a-2}{(a+2)(a-2)}$,
=$\frac{1}{a+2}$;
(3)原式=$\frac{{x}^{2}+1}{x-2}$+$\frac{3-4x}{x-2}$,
=$\frac{{x}^{2}-4x+4}{x-2}$,
=$\frac{(x-2)^{2}}{x-2}$,
=x-2;
(4)原式=[$\frac{1}{x(x-2)}$-$\frac{1}{(x-2)^{2}}$]•$\frac{x(x-2)}{2}$,
=[$\frac{x-2}{x(x-2)^{2}}$-$\frac{x}{x(x-2)^{2}}$]•$\frac{x(x-2)}{2}$,
=$\frac{-2}{x(x-2)^{2}}$]•$\frac{x(x-2)}{2}$,
=-$\frac{1}{x-2}$.
点评 此题主要考查了分式的混合运算,关键是要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

 小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?
小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?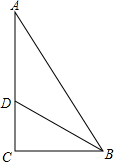 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.