题目内容
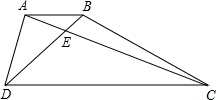 如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求:
如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求:(1)△ABE与△CDE的周长比;
(2)梯形ABCD的面积.
考点:相似三角形的判定与性质
专题:
分析:(1)易证△ABE∽△CDE,由相似三角形的性质:周长之比等于相似比即可得到问题答案;
(2)根据等高不等底的三角形面积之比等于底之比即可求出梯形ABCD的面积.
(2)根据等高不等底的三角形面积之比等于底之比即可求出梯形ABCD的面积.
解答:解:(1)∵AB∥CD,
∴△ABE∽△CDE,
∵CE:AE=3:1,
∴△ABE与△CDE的周长比为1:3;
(2)∵S△ADE=6cm2,DE:BE=3:1,
∴S△ABE=2cm2,S△DEC=18cm2
∴S△BEC=6cm2,
∴梯形ABCD的面积=6+6+2+18=32cm2.
∴△ABE∽△CDE,
∵CE:AE=3:1,
∴△ABE与△CDE的周长比为1:3;
(2)∵S△ADE=6cm2,DE:BE=3:1,
∴S△ABE=2cm2,S△DEC=18cm2
∴S△BEC=6cm2,
∴梯形ABCD的面积=6+6+2+18=32cm2.
点评:本题考查了相似三角形的判定和性质,解题的关键是掌握等高不等底的三角形面积之比等于底之比.

练习册系列答案
相关题目
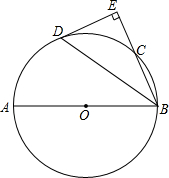 如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E.
如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC交BC的延长线于点E. 如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于
如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于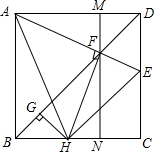 已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD. 如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)
如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)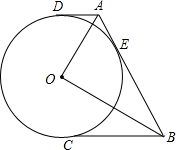 如图,已知∠AOB=90°,AD,AB,BC分别切⊙O于点D,E,C,⊙O半径为R,当点E在半圆DC上移动时,AD•BC的值是否变化,说明理由;若不变化,求出它的值.
如图,已知∠AOB=90°,AD,AB,BC分别切⊙O于点D,E,C,⊙O半径为R,当点E在半圆DC上移动时,AD•BC的值是否变化,说明理由;若不变化,求出它的值.