题目内容
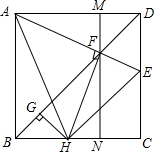 已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.(1)求证:AF=FH;
(2)求证:BD=2GF.
考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:证明题
分析:(1)延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
(2)连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG.
(2)连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG.
解答:证明:(1)连接FC,延长HF交AD于点L,
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC,
∴FH=AF;
(2)连接AC交BD于点O,可知:BD=2OA,
∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.

∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC,
∴FH=AF;
(2)连接AC交BD于点O,可知:BD=2OA,

∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
点评:本题考查了等腰三角形的判定和性质、全等三角形的判定和性质和正方形的性质,解答本题要充分利用正方形的特殊性质,在解题过程中要多次利用三角形全等是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列运算中,正确的是( )
| A、4a-3a=1 |
| B、a•a2=a3 |
| C、3a6÷a3=3a2 |
| D、(ab3)3=a3b6 |
若(x+a)(x+b)=x2+px+q,且p>0,q<0,那么a、b必须满足的条件是( )
| A、a、b都是正数 |
| B、a、b异号,且正数的绝对值较大 |
| C、a、b都是负数 |
| D、a、b异号,且负数的绝对值较大 |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
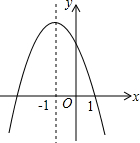 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )| A、3个 | B、4个 | C、5个 | D、6个 |
已知等腰三角形一边长为4,周长为10,则另两边长分别为( )
| A、4,2 | B、3,3 |
| C、4,2或3,3 | D、以上都不对 |
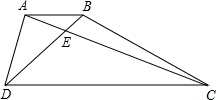 如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求:
如图,在梯形ABCD中,AB∥CD,AC、BD相交于点E,且CE:AE=3:1,S△ADE=6cm2,试求:
 如图,正方形ABFG和正方形CDEF顶点的边长为1的正方形格点上建立平面直角坐标系,使点B、C的坐标分别为(0,0)和(5,0),写出点A、D、E、F、G的坐标.
如图,正方形ABFG和正方形CDEF顶点的边长为1的正方形格点上建立平面直角坐标系,使点B、C的坐标分别为(0,0)和(5,0),写出点A、D、E、F、G的坐标.