题目内容
19.化简:$\frac{x+3}{{x}^{2}-1}÷\frac{{x}^{2}+6x+9}{{x}^{2}-2x+1}+\frac{1}{x+1}$.分析 原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算,约分即可得到结果.
解答 解:原式=$\frac{x+3}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{(x+3)^{2}}$+$\frac{1}{x+1}$=$\frac{x-1}{(x+1)(x+3)}$+$\frac{x+3}{(x+1)(x+3)}$=$\frac{2(x+1)}{(x+1)(x+3)}$=$\frac{2}{x+3}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
10.在△ABC中,如果$∠A=\frac{1}{2}∠B=\frac{1}{6}∠C$,则这个三角形一定是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
7.二次函数y=-(x-2)2-1的图象的顶点坐标是( )
| A. | (2,-1) | B. | (-2,-1) | C. | (-2,1) | D. | (2,1) |
20. 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )| A. | 132° | B. | 134° | C. | 136° | D. | 138° |
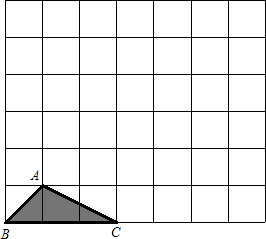 按要求完成作图.
按要求完成作图. 如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.
如图,图形2可以看作图形1先向下平移2格,再向左平移1格得到.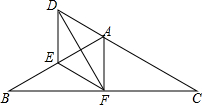 如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.