Question

4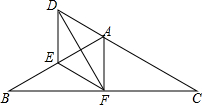．如图，△ABC中，AB=AC=6，F为BC的中点，D为CA延长线上一点，∠DFE=∠B．
（1）求证：$\frac{CD}{DF}$=$\frac{BF}{EF}$；
（2）若EF∥CD，求DE的长度．

Answer 1

分析 （1）根据外角的性质得到∠EFB=∠FDC，由等腰三角形的性质得到∠C=∠B，证得△CDF∽△BFE，根据相似三角形的性质得到$\frac{CD}{DF}=\frac{BF}{EF}$；
（2）根据平行线的性质得到∠EFD=∠FDC，∠C=∠EFB，根据等腰三角形的性质得到∠B=∠C，等量代换得到∠FDC=∠C，推出DF=CF，得到BF=DF，推出△DFE≌△BFE，根据全等三角形的性质得到结论．

解答 （1）证明：∵∠DFB=∠DFE+∠EFB=∠C+∠FDC，
∴∠EFB=∠FDC，
∵AB=AC，
∴∠C=∠B，
∴△CDF∽△BFE，
∴$\frac{CD}{DF}=\frac{BF}{EF}$；

（2）解：∵EF∥CD，
∴∠EFD=∠FDC，∠C=∠EFB，
∵AB=AC，
∴∠B=∠C，
∴∠FDC=∠C，
∴DF=CF，
∴BF=DF，
∴EF=$\frac{1}{2}$AC=3，∠DFE=∠BFE，
在△DFE与△BFE中，
$\left\{\begin{array}{l}{DF=BF}\\{∠DFE=∠BFE}\\{EF=EF}\end{array}\right.$，
∴△DFE≌△BFE，
∴DE=BE=3．

点评 本题考查了相似三角形的判定和性质，全等三角形的判定和性质，平行线的性质，熟练掌握相似三角形的判定和性质是解题的关键．