题目内容
3.化简:($\frac{x-3}{{x}^{2}-2x-3}-\frac{x}{{x}^{2}-1}$)$÷\frac{1}{x+1}$,并求x=$\frac{1}{3}$时的值.分析 首先根据分式化简的方法,把分式($\frac{x-3}{{x}^{2}-2x-3}-\frac{x}{{x}^{2}-1}$-)$÷\frac{1}{x+1}$进行化简,然后把x=$\frac{1}{3}$代入化简后的算式,求出算式的值是多少即可.
解答 解:($\frac{x-3}{{x}^{2}-2x-3}-\frac{x}{{x}^{2}-1}$)$÷\frac{1}{x+1}$
=[$\frac{x-3}{(x-3)(x+1)}$-$\frac{x}{(x-1)(x+1)}$]$÷\frac{1}{x+1}$
=[$\frac{1}{x+1}$-$\frac{x}{(x-1)(x+1)}$]$÷\frac{1}{x+1}$
=[$\frac{x-1}{(x-1)(x+1)}$-$\frac{x}{(x-1)(x+1)}$]$÷\frac{1}{x+1}$
=[-$\frac{1}{(x-1)(x+1)}$]$÷\frac{1}{x+1}$
=$\frac{1}{1-x}$
当x=$\frac{1}{3}$时,
原式=$\frac{1}{1-x}$=$\frac{1}{1-\frac{1}{3}}$=1$\frac{1}{2}$.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 互为相反数的两个数的绝对值相等 | |
| B. | 最小的整数是0 | |
| C. | 有理数分为正数和负数 | |
| D. | 如果两个数的绝对值相等,那么这两个数相等 |
15.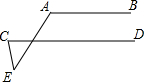 如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
 如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )| A. | 60° | B. | 80° | C. | 75° | D. | 70° |
12.甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.
(1)请你根据图中的数据填写表格:
(2)从平均数和方差相结合看,分析谁的成绩好些?从发展趋势来看,谁的成绩好些.

(1)请你根据图中的数据填写表格:
| 姓名 | 平均数 | 众数 | 方差 |
| 甲 | 8 | 8 | 0.4 |
| 乙 | 8 | 8 | 2.8 |
 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,若AB=6,AC=5,则△ADE的周长为( )