题目内容
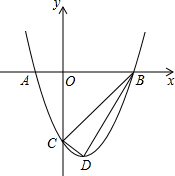 如图,已知抛物线y=ax2+bx+c 与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线x=1.
如图,已知抛物线y=ax2+bx+c 与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C(0,-3),其顶点为D,对称轴为直线x=1.(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标;
(3)将△OBC沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形△EFG,将△EFG与△BCD重叠部分的面积为S,用含m的代数式表示S.
考点:二次函数综合题
专题:
分析:(1)由抛物线 的对称轴为直线x=1.与x轴的一个交点为A的坐标,可得与x轴的另一个交点为B的坐标,再把三点代入y=ax2+bx+c 求解即可,
(2)分两种情况当AC=CM时,②当AC=CM时,分别求解即可,
(3)先求出直线BC与BD的解析式,再分两种情况①当0<m≤
时,②当
<m<3时求解即可.
(2)分两种情况当AC=CM时,②当AC=CM时,分别求解即可,
(3)先求出直线BC与BD的解析式,再分两种情况①当0<m≤
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:∵抛物线y=ax2+bx+c 的对称轴为直线x=1.与x轴的一个交点为A(-1,0),
∴与x轴的另一个交点为B(3,0),
∵与y轴的交点为C(0,-3),
∴
,
解得
.
∴抛物线的解析式为y=x2-2x-3.
(2)①当AC=AM时,M(0,3),
②当AC=CM时,M(0,-
-3)或M(0,
-3),
所以点M的坐标为(0,3),(0,-
-3)或M(0,
-3),
(3)记平移后的三角形为△EFG,设直线BC的解析式为y=kx+b,
则
,解得
,
则直线BC的解析式为y=x-3,
∵△OBC沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形△EFG,
∴易得y=x-3-m,
设直线BD的解析式为y=k′x+b′,则
,解得
,
直线BD的解析式为y=2x-6,
连接CG,直线CG交BD于H,则H(
,-3),在△OBC沿x轴向右平移的过程中,
①当0<m≤
时,如图1所示,

设EG交BC于点P,GF交BD于点Q,
则CG=BF=m,BE=PE=3-m,联立
,解得
,
即点Q(3-m,-2m),
S=S△EFG-S△EPB-S△BFQ
=
-
(3-m)2-
m•2m,
=-
m2+3m,
②当
<m<3时,如图2所示,

设EG交BC于点P,交BD于点N,
则OE=m,BE=PE=3-m,
∵直线BD的解析式为y=2x-6,
∴当x=m时,y=2m-6,
∴点N(m,2m-6),
∴S=S△EBN-S△EPB
=
(3-m)(6-2m)-
(3-m)2,
=
(3-m)2,
=-
m2-3m+
,
综上所述:当
<m≤3时,S=-
m2+3m,当
<m<3时,S=-
m2-3m+
,
∴与x轴的另一个交点为B(3,0),
∵与y轴的交点为C(0,-3),
∴
|
解得
|
∴抛物线的解析式为y=x2-2x-3.
(2)①当AC=AM时,M(0,3),
②当AC=CM时,M(0,-
| 10 |
| 10 |
所以点M的坐标为(0,3),(0,-
| 10 |
| 10 |
(3)记平移后的三角形为△EFG,设直线BC的解析式为y=kx+b,
则
|
|
则直线BC的解析式为y=x-3,
∵△OBC沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形△EFG,
∴易得y=x-3-m,
设直线BD的解析式为y=k′x+b′,则
|
|
直线BD的解析式为y=2x-6,
连接CG,直线CG交BD于H,则H(
| 3 |
| 2 |
①当0<m≤
| 3 |
| 2 |

设EG交BC于点P,GF交BD于点Q,
则CG=BF=m,BE=PE=3-m,联立
|
|
即点Q(3-m,-2m),
S=S△EFG-S△EPB-S△BFQ
=
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
②当
| 3 |
| 2 |

设EG交BC于点P,交BD于点N,
则OE=m,BE=PE=3-m,
∵直线BD的解析式为y=2x-6,
∴当x=m时,y=2m-6,
∴点N(m,2m-6),
∴S=S△EBN-S△EPB
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 9 |
| 2 |
综上所述:当
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
点评:本题主要考查了二次函数的综合题,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
下列各式中,正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
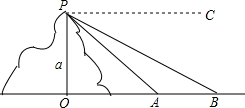 小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB.
小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB. 如图,已知双曲线y=
如图,已知双曲线y=
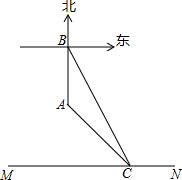 如图,某数学星期小组为了测量一东西走向的小河的宽度,设计了如下测量方案,先在北岸A处测得南岸一目标C在其东南方向,再向正北方向走50米到达B处,又测得目标C在其南偏东30°方向,请你根据以上测量结果计算小河的宽度(结果用根号表示).
如图,某数学星期小组为了测量一东西走向的小河的宽度,设计了如下测量方案,先在北岸A处测得南岸一目标C在其东南方向,再向正北方向走50米到达B处,又测得目标C在其南偏东30°方向,请你根据以上测量结果计算小河的宽度(结果用根号表示).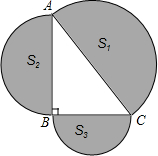 如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为
如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为