题目内容
16.简便计算:(1)20162-2015×2017;
(2)($\frac{1}{8}$)672×22017.
分析 (1)利用平方差公式进行计算,即可解答;
(2)利用幂的乘方和积的乘方进行计算,即可解答.
解答 解:(1)20162-2015×2017
=20162-(2016-1)×(2016+1)
=20162-(20162-1)
=21062-20162+1
=1.
(2)$(\frac{1}{8})^{672}×{2}^{2017}$
=$[(\frac{1}{2})^{3}]^{672}×{2}^{2017}$
=$(\frac{1}{2})^{2016}×{2}^{2017}$
=$(\frac{1}{2}×2)^{2016}×2$
=12016×2
=2.
点评 本题考查了平方差公式,解决本题的关键是熟记平方差公式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
| A. | (-2,-3) | B. | (-2,3) | C. | (2,-3) | D. | (2,3) |

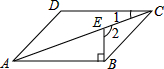 在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=25°,则∠2的度数为115°.
在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=25°,则∠2的度数为115°.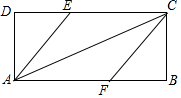 矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.
矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.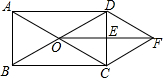 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证: