��Ŀ����
3�������ĸ����⣬����Ϊ��ȷ�������Ǣ٢ڢۣ�ֻ���������ţ��ټ���$\sqrt{18}$-$\sqrt{32}$+$\sqrt{2}$=0
����֪x1��x2�Ƿ���x2-2x-1=0������������$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-2
�۹���x��һԪ���η���x2-mx+��m-2��=0�� ��������ȵ�ʵ����
����xy��0����x+y��0����ô��P��x��y������ԭ��ĶԳƵ��ڵڶ����ޣ�
���� �ٻ�����θ�ʽ��
�����ø���ϵ���Ĺ�ϵ��ֵ��
�۸��ݸ����б�ʽ�ж�ʵ�����������
���ȸ�����֪����ȷ��x��y��ȡֵ��Ȼ�����жϹ���ԭ��ԳƵ�����ޣ�
��� �⣺
��ԭʽ=3$\sqrt{2}$-4$\sqrt{2}$+$\sqrt{2}$=0����ȷ��
�ڡ�x1+x2=2��x1•x2=-1����$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2}{-1}$=-2����ȷ��
�ۡ�=b2-4ac=��-m��2-4��1����m-2��=m2-4m+8=��m-2��2+4��0��
�������������ȵ�ʵ��������ȷ��
�ܡ�xy��0����x+y��0����x��0��y��0��
��P�����ԭ��ԳƵĵ��ڵ������ޣ�����
����ȷ�������Т٢ڢۣ�
���� ���������˶��θ�ʽ�Ļ���һԪ���η��̸���ϵ���Ĺ�ϵ�������б�ʽ������ϵ����������ԭ��ԳƵĵ��ȷ����

��ϰ��ϵ�д�
�����Ŀ
8����֪AE��CF����������ε������ߣ�AE��CF=2��3����sinA��sinC=��������
| A�� | 2��3 | B�� | 3��2 | C�� | 4��9 | D�� | 9��4 |
12�� һ����������ƽ��չ��ͼ��ͼ��ʾ����ô�ڸ��������к͡��塱��Ե����ǣ�������
һ����������ƽ��չ��ͼ��ͼ��ʾ����ô�ڸ��������к͡��塱��Ե����ǣ�������
 һ����������ƽ��չ��ͼ��ͼ��ʾ����ô�ڸ��������к͡��塱��Ե����ǣ�������
һ����������ƽ��չ��ͼ��ͼ��ʾ����ô�ڸ��������к͡��塱��Ե����ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | Т |
13������4cm��9cm��������ľ����β��ӣ�����һ�������ε�ľ���ǣ�������
| A�� | 4cm | B�� | 5cm | C�� | 9cm | D�� | 13cm |
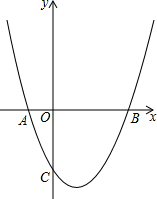 ��֪���κ���y=ax2+bx+c��a��0����ͼ���������ύ�������ֱ�ΪA��-1��0����B��3��0����C��0��-3����
��֪���κ���y=ax2+bx+c��a��0����ͼ���������ύ�������ֱ�ΪA��-1��0����B��3��0����C��0��-3����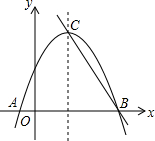 ��ͼ��������y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$��x���ཻ��A��B���㣬�����ߵĶ���ΪC���ʣ��������ߵĶԳ������Ƿ����һ��P��ʹ��P��x���ֱ��BC�����У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��ͼ��������y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$��x���ཻ��A��B���㣬�����ߵĶ���ΪC���ʣ��������ߵĶԳ������Ƿ����һ��P��ʹ��P��x���ֱ��BC�����У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�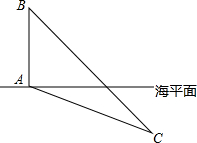 ��ij�ξ�����ϰ�У�����A���DZͧC�ĸ���Ϊ30�㣬λ�ھ���A���Ϸ�800m��ֱ����B���DZͧC�ĸ���Ϊ45�㣬�Ը��������������DZͧC�뿪��ƽ�����DZ��ȣ����������ȷֵ��
��ij�ξ�����ϰ�У�����A���DZͧC�ĸ���Ϊ30�㣬λ�ھ���A���Ϸ�800m��ֱ����B���DZͧC�ĸ���Ϊ45�㣬�Ը��������������DZͧC�뿪��ƽ�����DZ��ȣ����������ȷֵ��