题目内容
1.一块△ABC余料,已知AB=8cm,BC=15cm,AC=17cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是9π.分析 先利用勾股定理的逆定理证明△ABC为直角三角形,然后利用面积法求得圆的半径,最后利用圆的面积公式求解即可.
解答 解:∵AB=8cm,BC=15cm,AC=17cm,
∴AC2=AB2+BC2.
∴△ABC为直角三角形.
设△ABC的内切圆的半径为r,则$\frac{1}{2}AB•BC=\frac{1}{2}(AB+BC+AC)•r$,即$\frac{1}{2}×8×15=\frac{1}{2}×40×r$.
解得:r=3.
∴圆的最大面积是9π.
故答案为:9π.
点评 本题主要考查的是三角形的内切圆与内心、勾股定理的应用,明确三角形的面积=$\frac{1}{2}(AB+BC+AC)r$是解题的关键.

练习册系列答案
相关题目
12. 一个正方体其平面展开图如图所示,那么在该正方体中和“义”相对的字是( )
一个正方体其平面展开图如图所示,那么在该正方体中和“义”相对的字是( )
 一个正方体其平面展开图如图所示,那么在该正方体中和“义”相对的字是( )
一个正方体其平面展开图如图所示,那么在该正方体中和“义”相对的字是( )| A. | 礼 | B. | 智 | C. | 信 | D. | 孝 |
16.下列各对数中,互为相反数的一对数是( )
| A. | -23与-32 | B. | (-2)3与-23 | C. | (-3)2与-32 | D. | -(-1)与1 |
13.能与4cm,9cm长的两根木棒首尾相接,钉成一个三角形的木棒是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
10.关于旋转的性质,以下说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | |
| B. | 对应点与旋转中心所连线线段的夹角等于旋转角 | |
| C. | 旋转前、后的图形全等 | |
| D. | 对应点的连线必经过旋转中心且被旋转中心平分 |
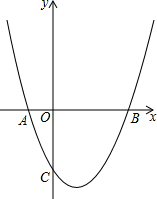 已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3).
已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3). 如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.
如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.