题目内容
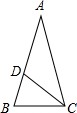 如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有
如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有考点:等腰三角形的判定
专题:
分析:根据三角形的内角和定理求出∠ACB,根据角平分线求出∠ACD=∠BCD=36°,求出∠BDC=72°,再根据等腰三角形的判定得出即可.
解答:解:有3个等腰三角形,
理由是:∵在△ABC中,∠A=36°,∠B=72°,
∴∠ACB=180°-∠A-∠B=72°,
∴∠ACB=∠B,
∴△ABC是等腰三角形,
∵CD是∠ACD的平分线,
∴∠ACD=∠BCD=
∠ACB=36°,
∴∠A=∠ACD=36°,
∴△ACD是等腰三角形,
∵∠BCD=36°,∠B=72°,
∴∠CDB=180°-36°-72°=72°,
∴∠B=∠CDB,
∴△BCD是等腰三角形,
故答案为:3.
理由是:∵在△ABC中,∠A=36°,∠B=72°,
∴∠ACB=180°-∠A-∠B=72°,
∴∠ACB=∠B,
∴△ABC是等腰三角形,
∵CD是∠ACD的平分线,
∴∠ACD=∠BCD=
| 1 |
| 2 |
∴∠A=∠ACD=36°,
∴△ACD是等腰三角形,
∵∠BCD=36°,∠B=72°,
∴∠CDB=180°-36°-72°=72°,
∴∠B=∠CDB,
∴△BCD是等腰三角形,
故答案为:3.
点评:本题考查了三角形的内角和定理,等腰三角形的判定的应用,解此题的关键是能求出各个角的度数,注意:有两角相等的三角形是等腰三角形.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
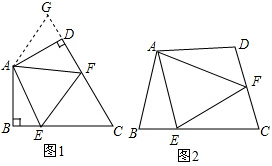
 把如图所示的图形沿虚线折叠,分别能折叠成什么几何体?观察制成的几何体,回答下列问题:
把如图所示的图形沿虚线折叠,分别能折叠成什么几何体?观察制成的几何体,回答下列问题: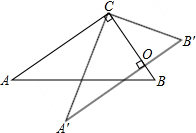 如图,在△ABC中,∠ACB=90°,将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,恰有BC与A′B′相交成直角,则图中与∠A互余的角有
如图,在△ABC中,∠ACB=90°,将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,恰有BC与A′B′相交成直角,则图中与∠A互余的角有 如图,直线AB,CD,EF相交于点O,已知∠AOC与∠COE互余,∠COE=25°,求∠BOD的度数.
如图,直线AB,CD,EF相交于点O,已知∠AOC与∠COE互余,∠COE=25°,求∠BOD的度数.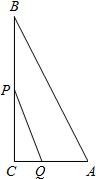 如图,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B以2cm/s的速度向点C移动,点Q以1cm/s的速度从点C向点A移动,如果点P,Q同时出发,则点P移动多少秒时△CPQ与△ABC相似?
如图,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B以2cm/s的速度向点C移动,点Q以1cm/s的速度从点C向点A移动,如果点P,Q同时出发,则点P移动多少秒时△CPQ与△ABC相似?