题目内容
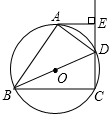 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;
(2)若AE=2,DE=1,求CD的长.
考点:切线的判定
专题:
分析:(1)连接OA,证明OA⊥AE即可.因为AE⊥CD,所以需证OA∥CE.根据角平分线定义和等腰三角形性质可证∠OAD=∠ODA=∠ADE可证;
(2)通过证明Rt△BAD∽Rt△AED,再利用对应边成比例关系从而求出⊙O半径的长..
(2)通过证明Rt△BAD∽Rt△AED,再利用对应边成比例关系从而求出⊙O半径的长..
解答: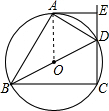 (1)证明:连接OA.
(1)证明:连接OA.
∵AO=DO,
∴∠OAD=∠ODA.
∵DA平分∠BDE,
∴∠ODA=∠EDA,
∴∠OAD=∠EDA.
∵∠EAD+∠EDA=90°,
∴∠EAD+∠OAD=90°,即∠OAE=90°.
∴OA⊥AE,
∴AE是⊙O的切线.
(2)解:在直角△ADE中,AD=
=
cm.
∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠AED=90°,∠ADE=∠ADB,
∴Rt△BAD∽Rt△AED.
∴
=
=
.
∴BD=
=5cm,AB=
=2
cm,
由切割线定理得:AE2=ED•EC,
∴EC=4,
∴CD=3.
 (1)证明:连接OA.
(1)证明:连接OA.∵AO=DO,
∴∠OAD=∠ODA.
∵DA平分∠BDE,
∴∠ODA=∠EDA,
∴∠OAD=∠EDA.
∵∠EAD+∠EDA=90°,
∴∠EAD+∠OAD=90°,即∠OAE=90°.
∴OA⊥AE,
∴AE是⊙O的切线.
(2)解:在直角△ADE中,AD=
| AE2+AD2 |
| 5 |
∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠AED=90°,∠ADE=∠ADB,
∴Rt△BAD∽Rt△AED.
∴
| DE |
| AD |
| AD |
| BD |
| AE |
| AB |
∴BD=
| AD2 |
| DE |
| AD•AE |
| DE |
| 5 |
由切割线定理得:AE2=ED•EC,
∴EC=4,
∴CD=3.
点评:本题考查切线的判定.已知直线经过圆上一点,证直线是圆的切线,需连接圆心和该点,证明直线与连线垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2011年我国国内生产总值(CDP)为471564亿元.471564用科学记数法表示为( )
| A、4.71564×l05 |
| B、4.71564×l04 |
| C、47.1564×l04 |
| D、0.471564×l06 |
 如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角.
如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角. 如图,⊙O1经过点A,B,⊙O2经过点A,B,点C是
如图,⊙O1经过点A,B,⊙O2经过点A,B,点C是
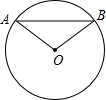 如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.
如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值. 如图,为了检查墙壁上的木条AB与水平线CD是否平行,小华测得∠1=108°,∠2=72°,问直线AB与CD平行吗?为什么?
如图,为了检查墙壁上的木条AB与水平线CD是否平行,小华测得∠1=108°,∠2=72°,问直线AB与CD平行吗?为什么? 如图,在正方形ABCD,∠EAF=45°,交BC、CD于E、F,交BD于H、G,求证:BG•DH为定值.
如图,在正方形ABCD,∠EAF=45°,交BC、CD于E、F,交BD于H、G,求证:BG•DH为定值.