题目内容
 如图,已知:A、F、C、D四点在一条直线上,AC=FD,∠D=∠A,且AB=DE.请将下面说明∠BFC=∠ECF的过程和理由补充完整.
如图,已知:A、F、C、D四点在一条直线上,AC=FD,∠D=∠A,且AB=DE.请将下面说明∠BFC=∠ECF的过程和理由补充完整.解:∵AC=FD(
∴AC-FC=FD-
即AF=DC.
在△ABF和△DEC中
AF=
∠A=∠D(
AB=
∴△ABF≌△DEC(
∴∠AFB=∠DCE(
∴∠BFC=∠ECF(
考点:全等三角形的判定与性质
专题:推理填空题
分析:求出AF=DC,根据SAS推出△ABF≌△DEC,推出∠AFB=∠DCE,根据等角的补角相等推出即可.
解答:解:∵AC=DF(已知),
∴AC-FC=FD-FC,
即AF=DC,
在△ABF和△DEC中
∴△ABF≌△DEC(SAS),
∴∠AFB=∠DCE(全等三角形的对应角相等),
∴∠BFC=∠ECF(等角的补角相等),
故答案为:已知,FC,DC,已知,DE,SAS,全等三角形的对应角相等,等角的补角相等.
∴AC-FC=FD-FC,
即AF=DC,
在△ABF和△DEC中
|
∴△ABF≌△DEC(SAS),
∴∠AFB=∠DCE(全等三角形的对应角相等),
∴∠BFC=∠ECF(等角的补角相等),
故答案为:已知,FC,DC,已知,DE,SAS,全等三角形的对应角相等,等角的补角相等.
点评:本题考查了等式的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力和理解能力.

练习册系列答案
相关题目
某农机厂四月份生产零件60万个,第二季度共生产零件189万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
| A、60(1+x)2=189 |
| B、60(1+2x)=189 |
| C、60+60(1+x)+60(1+x)2=189 |
| D、60+60(1+x)+60(1+2x)=189 |
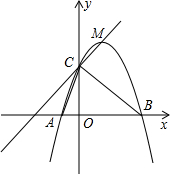 如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点.
如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点. 如图,O是直线AC上一点,OD平分∠AOB,∠BOE=
如图,O是直线AC上一点,OD平分∠AOB,∠BOE=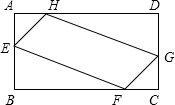 某学校校园内有如图的一块矩形ABCD空地,已知BC=20m,AB=10m,学校准备在这块空地的中间一块四边形EFGH内种花,其余部分铺设草坪,并要求AE=AH=CF=CG,四边形EFGH的种花面积为112m2,求AE的长.
某学校校园内有如图的一块矩形ABCD空地,已知BC=20m,AB=10m,学校准备在这块空地的中间一块四边形EFGH内种花,其余部分铺设草坪,并要求AE=AH=CF=CG,四边形EFGH的种花面积为112m2,求AE的长.