题目内容
 如图,O是直线AC上一点,OD平分∠AOB,∠BOE=
如图,O是直线AC上一点,OD平分∠AOB,∠BOE=| 1 |
| 2 |
考点:角的计算,角平分线的定义
专题:几何图形问题
分析:根据∠BOE=
∠COD可得:∠BOE=∠BOD+∠COE,再利用∠COE-∠BOD=40°与平角等于180°列等式计算.
| 1 |
| 2 |
解答:解:∵OD平分∠AOB,
∴∠AOD=∠BOD=
∠AOB,
∵∠BOE=
∠COD,
∴∠BOE=∠COE+∠DOB,
∠COE-∠BOD=∠BOE-∠AOB=40°①
∠COD+∠AOD=2∠BOE+
∠AOB=180°②
联立①②解得:∠BOE=80°
又∵∠COE+∠BOD=∠BOE=80°
∠COE-∠BOD=40°
∴∠BOD=20°
∴∠DOE=100°.
∴∠AOD=∠BOD=
| 1 |
| 2 |
∵∠BOE=
| 1 |
| 2 |
∴∠BOE=∠COE+∠DOB,
∠COE-∠BOD=∠BOE-∠AOB=40°①
∠COD+∠AOD=2∠BOE+
| 1 |
| 2 |
联立①②解得:∠BOE=80°
又∵∠COE+∠BOD=∠BOE=80°
∠COE-∠BOD=40°
∴∠BOD=20°
∴∠DOE=100°.
点评:此题主要考查角的基本运算和平角的灵活应用,要善于发现角之间的关系.属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

 如图,已知:A、F、C、D四点在一条直线上,AC=FD,∠D=∠A,且AB=DE.请将下面说明∠BFC=∠ECF的过程和理由补充完整.
如图,已知:A、F、C、D四点在一条直线上,AC=FD,∠D=∠A,且AB=DE.请将下面说明∠BFC=∠ECF的过程和理由补充完整.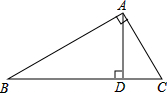 在△ABC中,∠BAC=90°,AB=8,AC=6,AD⊥BC,垂足为D,
在△ABC中,∠BAC=90°,AB=8,AC=6,AD⊥BC,垂足为D,