题目内容
15.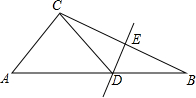 如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )| A. | 6 | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{2}$ | D. | 8 |
分析 由BC的中垂线交AB、BC于D、E,DE=3,BC=8,即可求得CD的长,又由AC=5,∠ACD=90°,即可求得答案.
解答 解:∵BC的中垂线交AB、BC于D、E,
∴CD=BD,CE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,∠CED=90°,
∵DE=3,
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=5,
∵AC=5,∠ACD=90°,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=5$\sqrt{2}$.
故选C.
点评 此题考查了线段垂直平分线的性质以及勾股定理.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
5.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在一次函数关系.从温度计的刻度上可以看出,摄氏温度x(℃)与华氏温度y(℉)有如下的对应关系:
(1)试确定y与x之间的函数关系式;
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
6.已知①x=1,②x-2=12,③x2+x+1=0,④xy=0,⑤2x+y=0,其中是一元一次方程的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
 如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.| A. | 32° | B. | 58° | C. | 68° | D. | 44° |