题目内容
3.观察下列各式及其化简过程:$\sqrt{7+2\sqrt{6}}=\sqrt{{1}^{2}+2\sqrt{1×6}+(\sqrt{6})^{2}}$=$\sqrt{(1+\sqrt{6})^{2}}=1+\sqrt{6}$;
$\sqrt{10-2\sqrt{21}}$=$\sqrt{(-3)^{2}-2\sqrt{3×7}+(\sqrt{7})^{2}}$=$\sqrt{(\sqrt{3}-\sqrt{7})^{2}}=\sqrt{7}-\sqrt{3}$.
(1)按照上述两个根式的化简过程的基本思想,化简$\sqrt{9+2\sqrt{14}}$;
(2)针对上述各式反映的规律,请你写出$\sqrt{a±2\sqrt{b}}$=$\sqrt{c}±\sqrt{d}$(c>d)中,a,b与c,d之间的关系.
分析 (1)直接利用完全平方公式将原式变形进而化简求出答案;
(2)直接利用已知结合完全平方公式求出答案.
解答 解:(1)由题意可得:$\sqrt{9+2\sqrt{14}}$=$\sqrt{(\sqrt{7}+\sqrt{2})^{2}}$=$\sqrt{7}$+$\sqrt{2}$;
(2)∵$\sqrt{a±2\sqrt{b}}$=$\sqrt{c}±\sqrt{d}$(c>d),
∴$\sqrt{a±2\sqrt{b}}$=$\sqrt{(\sqrt{c}±\sqrt{d})^{2}}$=$\sqrt{c+d+2\sqrt{cd}}$(c>d),
∴a=c+d,b=cd.
点评 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
8.2016年2月19日,经国务院批准,设立无锡市新吴区,将无锡市原新区的鸿山、旺庄、硕放、梅村、新安街道划和滨湖区的江溪街道归新吴区管辖.新吴区现有总人口322819人,这个数据用科学记数法(精确到千位)可表示为( )
| A. | 323×103 | B. | 3.22×105 | C. | 3.23×105 | D. | 0.323×106 |
14.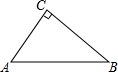 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
 如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
如图,∠ACB=90°,即AC⊥BC,若BC=8cm,AC=6cm,AB=10cm,那么B到AC的距离是8cm,A到BC的距离是6cm,A,B两点间的距离为10cm,C到AB的距离是4.8cm.
11.下列计算正确的是( )
| A. | $\sqrt{(-5)^{2}}=-5$ | B. | -($\sqrt{5}$)2=5 | C. | $\sqrt{25-4}=5-2$ | D. | -$\sqrt{\frac{5}{4}}=-\frac{\sqrt{5}}{2}$ |
18.已知$\sqrt{12a}$是整数,则正整数a的最小值是( )
| A. | 2 | B. | 3 | C. | 6 | D. | 12 |
8.下列各式是一元一次不等式的是( )
| A. | x2-3x+2>4x | B. | $\frac{1}{2}$x+2<x+3 | C. | $\frac{2}{x}$+1≤3x | D. | 2x+3=4x |
13.九年级数学兴趣小组经过市场调查,得到某种运动服进价为每件60元,每月的销量与售价的相关信息如表:
设该运动服的售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量y(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是(x-60)元,②月销量是(-2x+400)件.(直接写出结果);
(2)若要在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?
(3)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?