题目内容
7.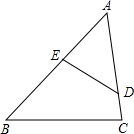 如图,由下列条件不能判定△ABC与△ADE相似的是( )
如图,由下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AD}$=$\frac{AC}{AB}$ | B. | ∠B=∠ADE | C. | $\frac{AE}{AC}$=$\frac{DE}{BC}$ | D. | ∠C=∠AED |
分析 利用两组对应边的比相等且夹角对应相等的两个三角形相似可对A、C进行判断;根据有两组角对应相等的两个三角形相似可对B、C进行判断.
解答 解:∵∠EAD=∠BAC,
∴当∠AED=∠C时,△AED∽△ACB;
当∠AED=∠B时,△AED∽△ABC;
当$\frac{AE}{AB}$=$\frac{AD}{AC}$时,△AED∽△ABC;
当$\frac{AE}{AC}$=$\frac{AD}{AB}$时,△AED∽△ACB.
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列各数中,最小的数是( )
| A. | -3 | B. | |-2| | C. | (-3)2 | D. | -22 |
12.用配方法解方程x2+4x+1=0,配方后的方程是( )
| A. | (x-2)2=5 | B. | (x+2)2=5 | C. | (x+2)2=3 | D. | (x-2)2=3 |
 如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是67.5°.
如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是67.5°.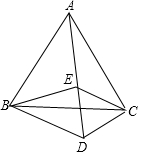 如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.
如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.