题目内容
17.一个不透明盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,求两次都摸到白球的概率是多少?分析 根据题意可以写出所有的可能性,从而可以得到两次都摸到白球的概率.
解答 解:由题意可得,
所有的可能性是:(红,绿)、(红、白),(红,白)、(绿,红)、(绿,白)、(绿,白)、(白,红)、(白,绿)、(白,白)、(白,红)、(白,绿)、(白,白),
∴两次都摸到白球的概率是:$\frac{2}{12}=\frac{1}{6}$,
即两次都摸到白球的概率是$\frac{1}{6}$.
点评 本题考查列表法与树状图法、概率,写出所有的可能性是解答此类题目的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
7.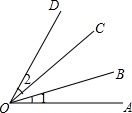 如图,若∠AOC=∠BOD,则有( )
如图,若∠AOC=∠BOD,则有( )
 如图,若∠AOC=∠BOD,则有( )
如图,若∠AOC=∠BOD,则有( )| A. | ∠1>∠2 | B. | ∠1<∠2 | ||
| C. | ∠1=∠2 | D. | ∠1与∠2的大小不能确定 |
8.若方程3(x-7)(x-2)=k的根是7和2,则k的值为( )
| A. | 0 | B. | 2 | C. | 7 | D. | 2或7 |
2.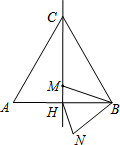 如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
 如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
如图,边长为4a的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )| A. | 2a | B. | a | C. | $\frac{1}{2}$a | D. | $\frac{1}{3}$a |
6. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )| A. | 15° | B. | 30° | C. | 38° | D. | 40° |
7.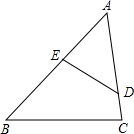 如图,由下列条件不能判定△ABC与△ADE相似的是( )
如图,由下列条件不能判定△ABC与△ADE相似的是( )
 如图,由下列条件不能判定△ABC与△ADE相似的是( )
如图,由下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AD}$=$\frac{AC}{AB}$ | B. | ∠B=∠ADE | C. | $\frac{AE}{AC}$=$\frac{DE}{BC}$ | D. | ∠C=∠AED |