题目内容
15. 在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.
在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.
分析 在直角三角形ACB中,先根据正切函数的定义求出BC=4,再利用勾股定理即可求出AB的值.
解答 解:∵在直角三角形ACB中,∠ACB=90°,AC=3,
∴tan∠B=$\frac{AC}{BC}$=$\frac{3}{BC}$=$\frac{3}{4}$,
∴BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题考查了解直角三角形,正切函数的定义,勾股定理,求出BC=4是解题的关键.

练习册系列答案
相关题目
5.计算(-a3)2的结果是( )
| A. | -a5 | B. | a5 | C. | -a6 | D. | a6 |
6. 如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
 如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )
如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果( )| A. | 15粒 | B. | 18粒 | C. | 20粒 | D. | 31粒 |
20.下列各式计算正确的是( )
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | 3a2•2a3=6a6 | D. | a8÷a2=a6 |
7.下列各数属于无理数的是( )
| A. | 5 | B. | $\sqrt{4}$ | C. | $\frac{7}{3}$ | D. | $\frac{π}{2}$ |
5.对于一组统计数据:3,4,2,2,4,下列说法错误的是( )
| A. | 中位数是3 | B. | 平均数是3 | C. | 方差是0.8 | D. | 众数是4 |
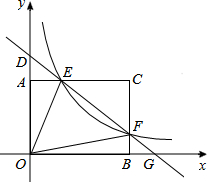 如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=$\frac{k}{x}$的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G,给出下列命题:
如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=$\frac{k}{x}$的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G,给出下列命题: