题目内容
4.先化简,再计算:$\frac{1-a2}{a2+a}÷(a-\frac{2a-1}{a})$,其中a是一元二次方程x2-2x-2=0的正数根.分析 先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 解:原式=$\frac{-(a+1)(a-1)}{a(a+1)}$÷$\frac{{a}^{2}-2a+1}{a}$
=$\frac{-(a-1)}{a}$•$\frac{a}{(a-1)^{2}}$
=$\frac{1}{1-a}$.
解x2-2x-2=0得,x1=1+$\sqrt{3}$,x1=1-$\sqrt{3}$,
∵a是一元二次方程x2-2x-2=0的正数根,
∴a=1+$\sqrt{3}$,
∴原式=$\frac{1}{1-1-\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
19.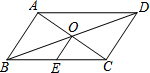 如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 12cm | B. | 9cm | C. | 6cm | D. | 3cm |
9.下列图形中,不能看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.用科学记数法表示0.0000907的结果正确的是( )
| A. | 9.1×10-4 | B. | 9.1×10-5 | C. | 9.0×10-5 | D. | 9.07×10-5 |
14.统计甲乙两人各10次射击的成绩发现,两人10次射击的平均成绩一样高,方差分别为S甲2=2,S乙2=5,则两人这10次射击成绩比较稳定的是( )
| A. | 甲 | B. | 乙 | C. | 两者一样稳定 | D. | 无法判断 |
 在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.
在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.