题目内容
7.下列各数属于无理数的是( )| A. | 5 | B. | $\sqrt{4}$ | C. | $\frac{7}{3}$ | D. | $\frac{π}{2}$ |
分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出属于无理数的是哪个即可.
解答 解:∵$\sqrt{4}=2$,5、2都是整数,
∴5、$\sqrt{4}$都是有理数;
∵$\frac{7}{3}=2.\stackrel{•}{3}$,2.$\stackrel{•}{3}$是循环小数,
∴$\frac{7}{3}$是有理数;
∵$\frac{π}{2}$是无限不循环小数,
∴$\frac{π}{2}$是无理数,
∴属于无理数的是$\frac{π}{2}$.
故选:D.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19.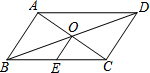 如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 12cm | B. | 9cm | C. | 6cm | D. | 3cm |
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b-1)x+c=0的一个根;(4)当-1<x<3时,ax2+(b-1)x+c>0.其中正确的个数为( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求AC、OA以及平行四边形ABCD的面积.
如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求AC、OA以及平行四边形ABCD的面积. 在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.
在直角三角形ACB中,∠ACB=90°,AC=3,tan∠B=$\frac{3}{4}$,求AB的值.