题目内容
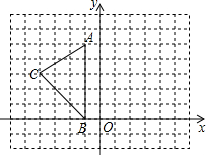 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).(1)求出△ABC的面积;
(2)将△ABC绕坐标原点顺时针旋转90°得△A′B′C′,并指出点A′,B′,C′的坐标.
考点:作图-旋转变换
专题:
分析:(1)根据△ABC的面积等于底边AB乘以AB边上的高列式计算即可;
(2)根据网格结构找出点A、B、C绕坐标原点顺时针旋转90°的对应点A′、B′、C′的位置,然后顺次连接即可.
(2)根据网格结构找出点A、B、C绕坐标原点顺时针旋转90°的对应点A′、B′、C′的位置,然后顺次连接即可.
解答:解:(1)∵A(-1,5),B(-1,0),C(-4,3),
∴AB=5,点C到AB的距离为-1-(-4)=3,
∴S△ABC=
×5×3=
;
(2)如图所示:
 ,
,
A'(5,1),B'(0,1),C'(3,4)).
∴AB=5,点C到AB的距离为-1-(-4)=3,
∴S△ABC=
| 1 |
| 2 |
| 15 |
| 2 |
(2)如图所示:
 ,
,A'(5,1),B'(0,1),C'(3,4)).
点评:本题考查了利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为( )
如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为( )| A、24cm2 |
| B、30cm2 |
| C、48cm2 |
| D、60cm2 |
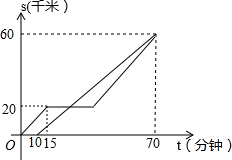 甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离S(千米)与时间t(分钟)的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
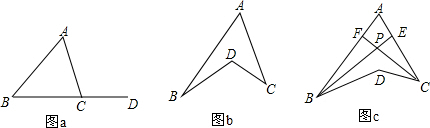
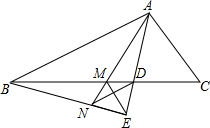 △ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.
△ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.