题目内容
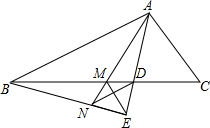 △ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.
△ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.(1)求证:∠BAC=2∠AEM;
(2)连接AM并延长交BE于N,连接DN,若AB=2AC.探究ME与DN的数量关系,并证明.
考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:(1)延长AC、BE相交于点F,根据角平分线的定义可得∠BAE=∠FAE,然后利用“角边角”证明△ABE和△AFE全等,根据全等三角形对应边相等可得BE=EF,AB=AF,从而得到ME是△BCF的中位线,根据三角形的中位线平行于第三边并且等于第三边的一可得ME∥AF,ME=
CF,再根据两直线平行,内错角相等可得∠AEM=∠FAE,从而得证;
(2)先求出AC=AF,再求出△MNE和△ANF相似,根据相似三角形对应边成比例求出
=
=
,再求出AB=4ME,
=
,再求出
=
,然后得到DN∥AB,然后根据平行线分线段成比例定理求出
=
,再求出AB=3DN,从而得解.
| 1 |
| 2 |
(2)先求出AC=AF,再求出△MNE和△ANF相似,根据相似三角形对应边成比例求出
| NE |
| NF |
| ME |
| AF |
| 1 |
| 4 |
| NE |
| BN |
| 1 |
| 2 |
| DE |
| AD |
| 1 |
| 2 |
| DN |
| AB |
| 1 |
| 3 |
解答:(1)证明:如图,延长AC、BE相交于点F,
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∵BE⊥AD,
∴∠AEB=∠AEF=90°,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵M为BC中点,
∴ME是△BCF的中位线,
∴ME∥AF,ME=
CF,
∴∠AEM=∠FAE,
∵AD平分∠BAC,
∴∠BAC=2∠FAE,
∴∠BAC=2∠AEM;
(2)解:4ME=3DN.
理由如下:∵AB=2AC,AB=AF,
∴AC=AF,
由ME∥AF得,△MNE∽△ANF,
∴
=
=
=
=
,
∴AB=AF=4ME,NE=4NF,
∴BE=EF=3NE,
∵ME∥AF,
∴
=
=
,
∴
=
=
,
∴DN∥AB,
∴
=
=
,
∴AB=3DN,
∴4ME=3DN.
∵AD平分∠BAC,
∴∠BAE=∠FAE,
∵BE⊥AD,
∴∠AEB=∠AEF=90°,
在△ABE和△AFE中,
|
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,

∵M为BC中点,
∴ME是△BCF的中位线,
∴ME∥AF,ME=
| 1 |
| 2 |
∴∠AEM=∠FAE,
∵AD平分∠BAC,
∴∠BAC=2∠FAE,
∴∠BAC=2∠AEM;
(2)解:4ME=3DN.
理由如下:∵AB=2AC,AB=AF,
∴AC=AF,
由ME∥AF得,△MNE∽△ANF,
∴
| NE |
| NF |
| ME |
| AF |
| ME |
| 2CF |
| ME |
| 2•2ME |
| 1 |
| 4 |
∴AB=AF=4ME,NE=4NF,
∴BE=EF=3NE,
∵ME∥AF,
∴
| DE |
| AD |
| ME |
| AC |
| 1 |
| 2 |
∴
| DE |
| AD |
| NE |
| BN |
| 1 |
| 2 |
∴DN∥AB,
∴
| DN |
| AB |
| NE |
| BE |
| 1 |
| 3 |
∴AB=3DN,
∴4ME=3DN.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,全等三角形的判定与性质,相似三角形的判定与性质,平行线分线段成比例定理,熟记各性质与定理并作出辅助线是解题的关键,难点在于(2)求出DN∥AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
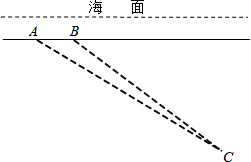 如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31.0°≈0.51,cos31.0°≈0.87,tan31.0°≈0.60)
如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31.0°≈0.51,cos31.0°≈0.87,tan31.0°≈0.60)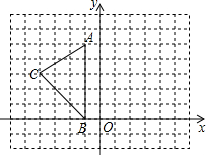 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).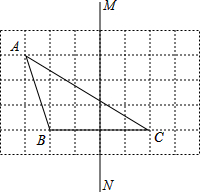 如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上.
如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上. 如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).
如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).
 如图,在Rt△ABC中,∠C=90°,BC=9,AC=12,点D在边AC上,且CD=
如图,在Rt△ABC中,∠C=90°,BC=9,AC=12,点D在边AC上,且CD=