题目内容
我们知道,由平行线可得出“同位角相等”,“内错角相等”等结论,因此,在几何证明中,我们往往可以通过添加平行线得到一些相等的角.
(1)如图a,点D在△ABC边BC的延长线上,请你猜想∠ACD与∠A、∠B之间的数量关系,并请你在图中通过添加平行线的方法,证明你的猜想.猜想结论是 证明:
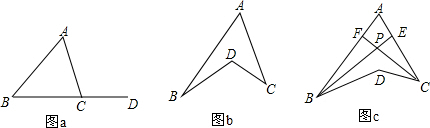
(2)如图b,四边形ABCD为一个凹四边形,请你利用(1)中你猜想的结论,求证:∠BDC=∠A+∠B+∠C;
(3)如图c,已知BE平分∠ABD,CF平分∠ACD,BE与CF相交于点P,当∠BDC=130°,∠BAC=60°时,求∠EPC的度数.
(1)如图a,点D在△ABC边BC的延长线上,请你猜想∠ACD与∠A、∠B之间的数量关系,并请你在图中通过添加平行线的方法,证明你的猜想.猜想结论是

(2)如图b,四边形ABCD为一个凹四边形,请你利用(1)中你猜想的结论,求证:∠BDC=∠A+∠B+∠C;
(3)如图c,已知BE平分∠ABD,CF平分∠ACD,BE与CF相交于点P,当∠BDC=130°,∠BAC=60°时,求∠EPC的度数.
考点:平行线的性质
专题:
分析:(1)过点C作CE∥AB,根据两直线平行,内错角相等可得∠A=∠ACE,两直线平行,同位角相等可得∠B=∠ECD,然后根据∠ACD=∠ACE+∠ECD等量代换即可得证;
(2)延长BD交AC于E,根据(1)的结论证明即可;
(3)根据(2)的结论求出∠ABD+∠ACD,再根据角平分线的定义求出∠PBD+∠PCD,然后再次利用结论计算求出∠BPC,再根据邻补角的定义计算即可得解.
(2)延长BD交AC于E,根据(1)的结论证明即可;
(3)根据(2)的结论求出∠ABD+∠ACD,再根据角平分线的定义求出∠PBD+∠PCD,然后再次利用结论计算求出∠BPC,再根据邻补角的定义计算即可得解.
解答:(1)解: 如图,过点C作CE∥AB,
如图,过点C作CE∥AB,
则∠A=∠ACE,∠B=∠ECD,
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B;
故答案为:∠ACD=∠A+∠B.
(2)证明:如图,延长BD交AC于E,
在△ABE中,∠CED=∠A+∠B,
在△CDE中,∠BDC=∠CED+∠C,
∴∠BDC=∠A+∠B+∠C;
(3)解:∵∠BDC=130°,∠BAC=60°,
∴∠ABD+∠ACD=130°-60°=70°,
∵BE平分∠ABD,CF平分∠ACD,
∴∠PBD+∠PCD=
(∠ABD+∠ACD)=
×70°=35°,
∴∠BPC=∠BDC-(∠PBD+∠PCD)=130°-35°=95°,
∴∠EPC=180°-∠BPC=180°-95°=85°.
 如图,过点C作CE∥AB,
如图,过点C作CE∥AB,则∠A=∠ACE,∠B=∠ECD,
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B;
故答案为:∠ACD=∠A+∠B.
(2)证明:如图,延长BD交AC于E,
在△ABE中,∠CED=∠A+∠B,
在△CDE中,∠BDC=∠CED+∠C,
∴∠BDC=∠A+∠B+∠C;
(3)解:∵∠BDC=130°,∠BAC=60°,
∴∠ABD+∠ACD=130°-60°=70°,
∵BE平分∠ABD,CF平分∠ACD,
∴∠PBD+∠PCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BPC=∠BDC-(∠PBD+∠PCD)=130°-35°=95°,
∴∠EPC=180°-∠BPC=180°-95°=85°.
点评:本题考查了平行线的性质,主要是三角形外角性质的证明,读懂题目信息,理解提供的求解方法和思路是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
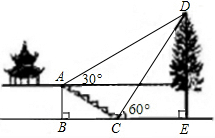 如图,兰州市某中学数学课题学习小组在“测量物体高度”的活动中,欲测量某公园内一棵古树DE的高度,他们在这棵古树的正前方一座楼亭前的台阶上A点处测得古树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得古树顶端D的仰角为60°.已知AB⊥BE于点B,且AB为4米,台阶AC的坡度为1:
如图,兰州市某中学数学课题学习小组在“测量物体高度”的活动中,欲测量某公园内一棵古树DE的高度,他们在这棵古树的正前方一座楼亭前的台阶上A点处测得古树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得古树顶端D的仰角为60°.已知AB⊥BE于点B,且AB为4米,台阶AC的坡度为1: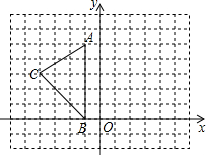 如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3). 如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,全长68km.现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据: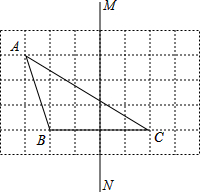 如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上.
如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上.