题目内容
19.x1、x2是方程x2+ax+b=0的两根,若△=8,并且$\frac{{x}_{1}}{{x}_{2}}$=$\frac{3}{4}$,求此方程的两个根.分析 首先根据根与系数的关系得到x1+x2=-a,x1x2=b,结合△=8和$\frac{{x}_{1}}{{x}_{2}}$=$\frac{3}{4}$列出$\frac{16{a}^{2}}{49}$=$\frac{4b}{3}$①和a2-4b=8②两个方程,解方程求出a和b的值,进而求出方程的两个根.
解答 解:∵x1、x2是方程x2+ax+b=0的两根,
∴x1+x2=-a,x1x2=b,
∵$\frac{{x}_{1}}{{x}_{2}}=\frac{3}{4}$,
∴4x1=3x2,
∴$\frac{3}{4}$x2+x2=-a,则x2=$\frac{-4a}{7}$,即x22=$\frac{16{a}^{2}}{49}$,
∴$\frac{3}{4}$x22=b,
∴$\frac{16{a}^{2}}{49}$=$\frac{4b}{3}$①,
∵△=8,
∴a2-4b=8②,
由①②解得:a=±14$\sqrt{2}$,b=96,
当a=14$\sqrt{2}$时,
x=$\frac{-14\sqrt{2}±2\sqrt{2}}{2}$,即x=-8$\sqrt{2}$或-6$\sqrt{2}$,
当a=-14$\sqrt{2}$时,
x=$\frac{14\sqrt{2}±2\sqrt{2}}{2}$,即x=8$\sqrt{2}$或6$\sqrt{2}$.
点评 本题主要考查了根与系数的关系以及根的判别式的知识,解答本题的关键是列出a和b的两个关系式,此题计算稍微有些麻烦,但是难度不大.

练习册系列答案
相关题目
7.一辆汽车从A地出发,向东行驶,途中要经过十字路口B,在规定的某一段时间内,若车速为每小时60千米,就能驶过B处2千米;若每小时行驶50千米,就差3千米才能到达B处,设A、B间的距离为x千米,规定的时间为y小时,则可列出方程组是( )
| A. | $\left\{\begin{array}{l}{60y-x=2}\\{x=3-50y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60y-x=2}\\{50y-x=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{60y=x+2}\\{50y=x-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60y=x-2}\\{50y=x+3}\end{array}\right.$ |
 中俄“海上联合”军事演习中,如图,海中有一个小岛A,它周围8.5海里内有暗礁,一艘舰艇由西向东航行,在D点测得小岛A在北偏东60°方向上,航行12海里到达B点,这时测得小岛北偏东30°方向上,请通过计算加以说明这嫂舰艇在B处开始是否需要调整航线,才能安全通过这一海域?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
中俄“海上联合”军事演习中,如图,海中有一个小岛A,它周围8.5海里内有暗礁,一艘舰艇由西向东航行,在D点测得小岛A在北偏东60°方向上,航行12海里到达B点,这时测得小岛北偏东30°方向上,请通过计算加以说明这嫂舰艇在B处开始是否需要调整航线,才能安全通过这一海域?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)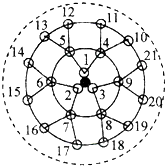 生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二产生新的微生物(依次标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么8天所出现的微生物中标号最大的数字是1533号.
生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二产生新的微生物(依次标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么8天所出现的微生物中标号最大的数字是1533号.