Question

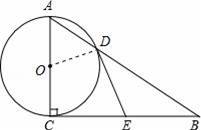
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．

（1）求证：EB=EC；

（2）若以点O、D、E、C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．

Answer 1

【考点】切线的性质；正方形的性质；圆周角定理．

【专题】证明题．

【分析】（1）连接OD，由BC是⊙O的切线得出∠BCA=90°，由DE是⊙O的切线，得出ED=EC，∠ODE=90°，故可得出∠EDB=∠EBD，由此可得出结论．

（2）当以点O、D、E、C为顶点的四边形是正方形时，则△DEB是等腰直角三角形，据此即可判断．

【解答】（1）证明：连接OD，

∵AC是直径，∠ACB=90°，

∴BC是⊙O的切线，∠BCA=90°．

又∵DE是⊙O的切线，

∴ED=EC，∠ODE=90°，

∴∠ODA+∠EDB=90°，

∵OA=OD，

∴∠OAD=∠ODA，

又∵∠OAD+∠DBE=90°，

∴∠EDB=∠EBD，

∴ED=EB，

∴EB=EC．

 

（2）解：当以点O、D、E、C为顶点的四边形是正方形时，则∠DEB=90°，

又∵ED=EB，

∴△DEB是等腰直角三角形，则∠B=45°，

∴△ABC是等腰直角三角形．

【点评】本题考查了切线的性质以及切线长定理、圆周角定理，解题的关键是连接OD得垂直，构造出等腰三角形，利用“等角的余角相等解答．