题目内容
先阅读再解题．
题目：如果（x﹣1）5=a1x5+a2x4+a3x3+a4x2+a5x+a6，求a6的值．
解这类题目时，可根据等式的性质，取x的特殊值，如x=0，1，﹣1…代入等式两边即可求得有关代数式的值．如：当x=0时，（0﹣1）5=a6，即a6=1．
请你求出下列代数式的值．
（1）a1+a2+a3+a4+a5
（2）a1﹣a2+a3﹣a4+a5．
【考点】代数式求值．
【分析】（1）令x=1，可得a1+a2+a3+a4+a5+a6，由a6=1可得结果；
（2）令x=﹣1，可得﹣a1+a2﹣a3+a4﹣a5，易得结果．
【解答】解：（1）x=0时，（0﹣1）5=a6，即a6=1，
当x=1时，（1﹣1）2=a1+a2+a3+a4+a5+a6，
即a1+a2+a3+a4+a5=0﹣1=﹣1；
（2）当x=﹣1时，（﹣1﹣1）2=﹣a1+a2﹣a3+a4﹣a5+a6，
即﹣a1+a2﹣a3+a4﹣a5+a6=4，
∴a1﹣a2+a3﹣a4+a5=﹣3．
练习册系列答案
相关题目
B．
C．
D．
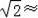
1.41，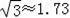
）
