Question

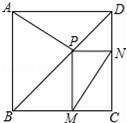
已知，如图，正方形ABCD，菱形EFGP，点E、F、G分别在AB、AD、CD上，延长DC，PH⊥DC于H．

（1）求证：GH=AE；

（2）若菱形EFGP的周长为20cm，，FD=2，求△PGC的面积．

Answer 1

【考点】菱形的性质；全等三角形的判定与性质；正方形的性质．

【专题】计算题；证明题．

【分析】（1）根据图形性质可证明△AEF≌△HGP，从而即得GH=AE．

（2）△PGC的面积=×GC×PH，而由（1）知PH=AF，再根据题中已知条件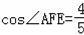及边长可求得边AD、AF和DG的长，从而得到GC的长，即可求得面积．

【解答】（1）证明：由菱形性质知：∠EFG+∠FGP=180°，EF=GP=EP=FG，

又∠AEF+∠AFE=90°，∠DFG+∠DGF=90°，∠AFE+∠EFG+∠DFG=180°，∠DGF+∠FGP+∠PGH=180°，

∴∠AFE=∠GPH，

又∵∠A=∠H，

∴△AEF≌△HGP，（AAS）

∴GH=AE；

 

（2）解：∵菱形EFGP的周长为20cm，

∴EF=GP=EP=FG=5cm，

又∵，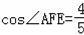

∴在△AEF中，AF=4，EF=5，

又∵FD=2，

∴正方形边长=AD=DC=6，

在△DFG中，DG==，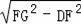

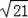
∴GC=6﹣，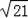

又由（1）知PH=AF，

∴△PGC的面积=×GC×PH=×GC×AF=12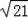﹣2（cm²）．

【点评】本题考查了正方形性质以及菱形性质，是基础题．