题目内容
18.先化简,再求值.$\frac{{x}^{2}-2xy+{y}^{2}}{2x-2y}$÷($\frac{1}{y}$-$\frac{1}{x}$),其中x=$\sqrt{5}$-1,y=$\sqrt{5}$+1.分析 先化简题目中的式子,然后将x、y的值代入化简后的式子即可解答本题.
解答 解:$\frac{{x}^{2}-2xy+{y}^{2}}{2x-2y}$÷($\frac{1}{y}$-$\frac{1}{x}$)
=$\frac{(x-y)^{2}}{2(x-y)}÷\frac{x-y}{xy}$
=$\frac{(x-y)^{2}}{2(x-y)}•\frac{xy}{x-y}$
=$\frac{xy}{2}$,
当x=$\sqrt{5}$-1,y=$\sqrt{5}$+1时,
原式=$\frac{(\sqrt{5}-1)(\sqrt{5}+1)}{2}$=$\frac{4}{2}$=2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
8. 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )
如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )
 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )
如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )| A. | 2平方厘米 | B. | 1平方厘米 | C. | $\frac{1}{2}$平方厘米 | D. | $\frac{1}{4}$平方厘米 |
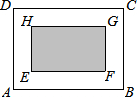 在一块长12m,宽8m的长方形平地中央,划出地方砌一个面积为32m2的长方形花台,要使花坛四周的宽地宽度一样,则这个宽度为多少?
在一块长12m,宽8m的长方形平地中央,划出地方砌一个面积为32m2的长方形花台,要使花坛四周的宽地宽度一样,则这个宽度为多少? 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,BC=9,求DE的长.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,BC=9,求DE的长.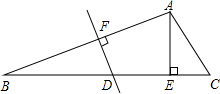 如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.
如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.